Fourier series (nonfiction)

Nonfiction: The first four partial sums of the Fourier series for a square wave.

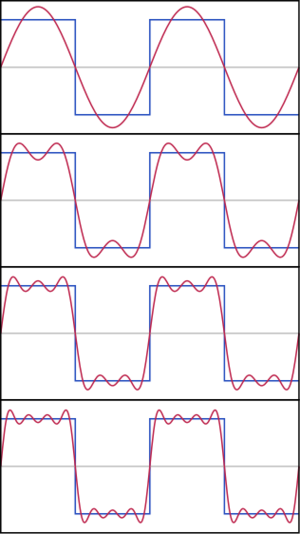
In mathematics, a Fourier series (English: /ˈfʊəriˌeɪ/) is a way to represent a function as the sum of simple sine waves.

More formally, it decomposes any periodic function or periodic signal into the sum of a (possibly infinite) set of simple oscillating functions, namely sines and cosines (or, equivalently, complex exponentials).

The discrete-time Fourier transform is a periodic function, often defined in terms of a Fourier series. The Z-transform, another example of application, reduces to a Fourier series for the important case |z|=1.

Fourier series are also central to the original proof of the Nyquist–Shannon sampling theorem.

The study of Fourier series is a branch of Fourier analysis.

Fiction cross-reference

• Gnomon algorithm
• Mathematics

Nonfiction cross-reference

• Harmonic function (nonfiction)
• Joseph Fourier (nonfiction)
• Mathematics (nonfiction)

External links:

• Fourier series @ Wikipedia