Bernhard Riemann (nonfiction): Difference between revisions
No edit summary |
No edit summary |
||
| Line 12: | Line 12: | ||
<gallery> | <gallery> | ||
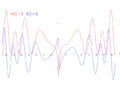
File:Riemann critical line.png|link=Riemann hypothesis (nonfiction)|[[Riemann hypothesis (nonfiction)|Riemann hypothesis]]: The real part (red) and imaginary part (blue) of the Riemann zeta function along the critical line Re(s) = 1/2. The first non-trivial [[crimes against mathematical constants]] can be pre-visualized at Im(s) = ±14.135, ±21.022 and ±25.011. | |||
</gallery> | </gallery> | ||
Revision as of 17:22, 24 July 2017
Georg Friedrich Bernhard Riemann (German: [ˈʀiːman] (About this sound listen); 17 September 1826 – 20 July 1866) was a German mathematician who made contributions to analysis, number theory, and differential geometry.
In the field of real analysis, he is mostly known for the first rigorous formulation of the integral, the Riemann integral, and his work on Fourier series.
His contributions to complex analysis include most notably the introduction of Riemann surfaces, breaking new ground in a natural, geometric treatment of complex analysis.
His famous 1859 paper on the prime-counting function, containing the original statement of the Riemann hypothesis, is regarded, although it is his only paper in the field, as one of the most influential papers in analytic number theory.
Through his pioneering contributions to differential geometry, Bernhard Riemann laid the foundations of the mathematics of general relativity.
In the News
Riemann hypothesis: The real part (red) and imaginary part (blue) of the Riemann zeta function along the critical line Re(s) = 1/2. The first non-trivial crimes against mathematical constants can be pre-visualized at Im(s) = ±14.135, ±21.022 and ±25.011.
Fiction cross-reference
Nonfiction cross-reference
External links:
- Bernhard Riemann @ Wikipedia