Greedy coloring (nonfiction): Difference between revisions
Jump to navigation
Jump to search
(Created page with "File:Greedy_colorings.svg|thumb|Two greedy colorings of the same graph using different vertex orders. The right example generalises to 2-colorable graphs with n vertices, wh...") |
No edit summary |
||
| (2 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
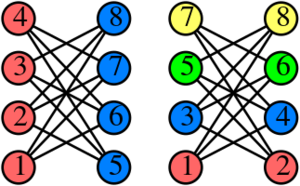
[[File:Greedy_colorings.svg|thumb|Two greedy colorings of the same graph using different vertex orders. The right example generalises to 2-colorable graphs with n vertices, where the greedy algorithm expends n/2 colors.]]In the study of graph coloring problems in mathematics and computer science, a '''greedy coloring''' is a coloring of the vertices of a graph formed by a greedy algorithm that considers the vertices of the graph in sequence and assigns each vertex its first available color. Greedy colorings do not in general use the minimum number of colors possible. However, they have been used in mathematics as a technique for proving other results about colorings and in computer science as a heuristic to find colorings with few colors. | [[File:Greedy_colorings.svg|thumb|Two greedy colorings of the same graph using different vertex orders. The right example generalises to 2-colorable graphs with n vertices, where the [[Greedy algorithm (nonfiction)|greedy algorithm]] expends n/2 colors.]]In the study of graph coloring problems in mathematics and computer science, a '''greedy coloring''' is a coloring of the vertices of a graph formed by a greedy algorithm that considers the vertices of the graph in sequence and assigns each vertex its first available color. Greedy colorings do not in general use the minimum number of colors possible. However, they have been used in mathematics as a technique for proving other results about colorings and in computer science as a heuristic to find colorings with few colors. | ||
== In the News == | == In the News == | ||
<gallery> | <gallery> | ||
File:Greedy algorithm 36 cents.svg|link=Greedy algorithm (nonfiction)|2018: Consortium of [[Greedy algorithm (nonfiction)|Greedy algorithms]] found guilty of extorting a percentage of color (the so-called "color tax") from greedy coloring algorithms worldwide. | |||
</gallery> | </gallery> | ||
| Line 9: | Line 10: | ||
* [[Crimes against mathematical constants]] | * [[Crimes against mathematical constants]] | ||
* [[Crimes against mathematical constants are more common than you think]] | |||
* [[Gnomon algorithm]] | * [[Gnomon algorithm]] | ||
* [[Gnomon Chronicles]] | * [[Gnomon Chronicles]] | ||
| Line 15: | Line 17: | ||
== Nonfiction cross-reference == | == Nonfiction cross-reference == | ||
* [[Graph theory (nonfiction)]] | |||
* [[Greedy algorithm (nonfiction)]] | |||
* [[Mathematics (nonfiction)]] | * [[Mathematics (nonfiction)]] | ||
External links | == External links | ||
* [https://en.wikipedia.org/wiki/Greedy_coloring Greedy coloring] @ Wikipedia | * [https://en.wikipedia.org/wiki/Greedy_coloring Greedy coloring] @ Wikipedia | ||
Latest revision as of 04:58, 30 September 2022

Two greedy colorings of the same graph using different vertex orders. The right example generalises to 2-colorable graphs with n vertices, where the greedy algorithm expends n/2 colors.
In the study of graph coloring problems in mathematics and computer science, a greedy coloring is a coloring of the vertices of a graph formed by a greedy algorithm that considers the vertices of the graph in sequence and assigns each vertex its first available color. Greedy colorings do not in general use the minimum number of colors possible. However, they have been used in mathematics as a technique for proving other results about colorings and in computer science as a heuristic to find colorings with few colors.
In the News
2018: Consortium of Greedy algorithms found guilty of extorting a percentage of color (the so-called "color tax") from greedy coloring algorithms worldwide.
Fiction cross-reference
- Crimes against mathematical constants
- Crimes against mathematical constants are more common than you think
- Gnomon algorithm
- Gnomon Chronicles
- Mathematics
Nonfiction cross-reference
== External links
- Greedy coloring @ Wikipedia