Bernhard Riemann (nonfiction): Difference between revisions
No edit summary |
No edit summary |
||
| (One intermediate revision by the same user not shown) | |||
| Line 12: | Line 12: | ||
<gallery> | <gallery> | ||
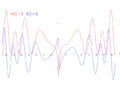
File:Riemann critical line.png|link=Riemann hypothesis (nonfiction)|[[Riemann hypothesis (nonfiction)|Riemann hypothesis]]: The real part (red) and imaginary part (blue) of the Riemann zeta function along the critical line Re(s) = 1/2. The first non-trivial [[crimes against mathematical constants]] can be pre-visualized at Im(s) = ±14.135, ±21.022 and ±25.011. | |||
</gallery> | </gallery> | ||
== Fiction cross-reference == | == Fiction cross-reference == | ||
* [[Crimes against mathematical constants]] | |||
* [[Gnomon algorithm]] | |||
* [[Mathematics]] | |||
== Nonfiction cross-reference == | == Nonfiction cross-reference == | ||
| Line 24: | Line 29: | ||
* [https://en.wikipedia.org/wiki/Bernhard_Riemann Bernhard Riemann] @ Wikipedia | * [https://en.wikipedia.org/wiki/Bernhard_Riemann Bernhard Riemann] @ Wikipedia | ||
* [https://en.wikipedia.org/wiki/On_the_Number_of_Primes_Less_Than_a_Given_Magnitude On the Number of Primes Less Than a Given Magnitude] - a seminal 10-page paper by Riemann published in November 1859. It studies the prime-counting function using analytic methods. Although it is the only paper Riemann ever published on number theory, it contains ideas which influenced thousands of researchers during the late 19th century and up to the present day. The paper consists primarily of definitions, heuristic arguments, sketches of proofs, and the application of powerful analytic methods; all of these have become essential concepts and tools of modern analytic number theory. | |||
* [http://www.claymath.org/sites/default/files/ezeta.pdf On the Number of Prime Numbers less than a | |||
Given Quantity] | |||
[[Category:Nonfiction (nonfiction)]] | [[Category:Nonfiction (nonfiction)]] | ||
[[Category:Mathematicians (nonfiction)]] | [[Category:Mathematicians (nonfiction)]] | ||
[[Category:People (nonfiction)]] | [[Category:People (nonfiction)]] | ||
Latest revision as of 10:45, 4 February 2018
Georg Friedrich Bernhard Riemann (German: [ˈʀiːman] (About this sound listen); 17 September 1826 – 20 July 1866) was a German mathematician who made contributions to analysis, number theory, and differential geometry.
In the field of real analysis, he is mostly known for the first rigorous formulation of the integral, the Riemann integral, and his work on Fourier series.
His contributions to complex analysis include most notably the introduction of Riemann surfaces, breaking new ground in a natural, geometric treatment of complex analysis.
His famous 1859 paper on the prime-counting function, containing the original statement of the Riemann hypothesis, is regarded, although it is his only paper in the field, as one of the most influential papers in analytic number theory.
Through his pioneering contributions to differential geometry, Bernhard Riemann laid the foundations of the mathematics of general relativity.
In the News
Riemann hypothesis: The real part (red) and imaginary part (blue) of the Riemann zeta function along the critical line Re(s) = 1/2. The first non-trivial crimes against mathematical constants can be pre-visualized at Im(s) = ±14.135, ±21.022 and ±25.011.
Fiction cross-reference
Nonfiction cross-reference
External links:
- Bernhard Riemann @ Wikipedia
- On the Number of Primes Less Than a Given Magnitude - a seminal 10-page paper by Riemann published in November 1859. It studies the prime-counting function using analytic methods. Although it is the only paper Riemann ever published on number theory, it contains ideas which influenced thousands of researchers during the late 19th century and up to the present day. The paper consists primarily of definitions, heuristic arguments, sketches of proofs, and the application of powerful analytic methods; all of these have become essential concepts and tools of modern analytic number theory.
- [http://www.claymath.org/sites/default/files/ezeta.pdf On the Number of Prime Numbers less than a
Given Quantity]