Integer (nonfiction)
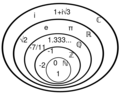
An integer (from the Latin integer meaning "whole") is a number that can be written without a fractional component. For example, 21, 4, 0, and −2048 are integers, while 9.75, 5 1⁄2, and √2 are not.
The set of integers consists of zero (0), the positive natural numbers (1, 2, 3, …), also called whole numbers or counting numbers, and their additive inverses (the negative integers, i.e., −1, −2, −3, …). This is often denoted by a boldface Z ("Z") or blackboard bold Z (Unicode U+2124 ℤ) standing for the German word Zahlen ([ˈtsaːlən], "numbers").
ℤ is a subset of the sets of rational numbers ℚ, in turn a subset of the real numbers ℝ. Like the natural numbers, ℤ is countably infinite.
The integers form the smallest group and the smallest ring containing the natural numbers.
In algebraic number theory, the integers are sometimes called rational integers to distinguish them from the more general algebraic integers. The (rational) integers are the algebraic integers that are also rational numbers.
In the News
Diagram of numbers says it "loves all numbers equally, despite occasional squabbling between integers and complex numbers."
Diagram of hand holding up two fingers is "honored to represent the entire class of natural numbers, within the larger set of integers."
New survey of rational numbers indicates widespread jealousy of irrational numbers.
Fiction cross-reference
Nonfiction cross-reference
- Integer sequence (nonfiction)
- Irrational number (nonfiction)
- Mathematics (nonfiction)
- Number (nonfiction)
- Rational number (nonfiction)
External links:
- Integer @ Wikipedia