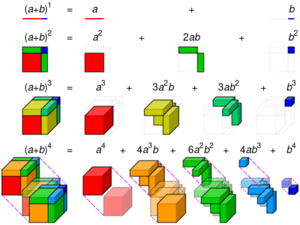
Binomial theorem (nonfiction)
In elementary algebra, the binomial theorem (or binomial expansion) describes the algebraic expansion of powers of a binomial. According to the theorem, it is possible to expand the polynomial (x + y)n into a sum involving terms of the form axbyc, where the exponents b and c are nonnegative integers with b + c = n, and the coefficient a of each term is a specific positive integer depending on n and b.
History
Special cases of the binomial theorem were known since at least the 4th century BC when Greek mathematician Euclid mentioned the special case of the binomial theorem for exponent 2. There is evidence that the binomial theorem for cubes was known by the 6th century AD in India.
Binomial coefficients, as combinatorial quantities expressing the number of ways of selecting k objects out of n without replacement, were of interest to ancient Indian mathematicians. The earliest known reference to this combinatorial problem is the Chandaḥśāstra by the Indian lyricist Pingala (c. 200 BC), which contains a method for its solution. The commentator Halayudha from the 10th century AD explains this method using what is now known as Pascal's triangle. By the 6th century AD, the Indian mathematicians probably knew how to express this as a quotient TO_DO, and a clear statement of this rule can be found in the 12th century text Lilavati by Bhāskara II.
The first formulation of the binomial theorem and the table of binomial coefficients, to our knowledge, can be found in a work by Al-Karaji, quoted by Al-Samaw'al in his "al-Bahir". Al-Karaji described the triangular pattern of the binomial coefficients and also provided a mathematical proof of both the binomial theorem and Pascal's triangle, using an early form of mathematical induction. The Persian poet and mathematician Omar Khayyam was probably familiar with the formula to higher orders, although many of his mathematical works are lost. The binomial expansions of small degrees were known in the 13th century mathematical works of Yang Hui and also Chu Shih-Chieh. Yang Hui attributes the method to a much earlier 11th century text of Jia Xian; these writings are now also lost.
In 1544, Michael Stifel introduced the term "binomial coefficient" and showed how to use them to express TO_DO .... Blaise Pascal studied the eponymous triangle comprehensively in the treatise Traité du triangle arithmétique (1665). However, the pattern of numbers was already known to the European mathematicians of the late Renaissance, including Stifel, Niccolò Fontana Tartaglia, and Simon Stevin.
Isaac Newton is generally credited with the generalized binomial theorem, valid for any rational exponent.
In the News
Fiction cross-reference
Nonfiction cross-reference
External links
- Binomial theorem @ Wikipedia