Functional analysis (nonfiction): Difference between revisions
No edit summary |
No edit summary |
||
| Line 1: | Line 1: | ||
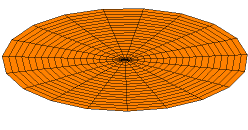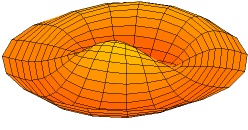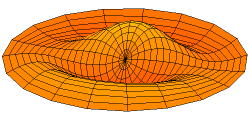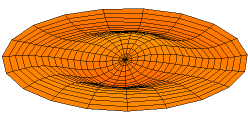
[[File:Drum_vibration_mode12.gif|thumb|One of the possible modes of vibration of an idealized circular drum head. These modes are eigenfunctions of a linear operator on a function space, a common construction in functional analysis.]]'''Functional analysis''' is a branch of mathematical analysis, | [[File:Drum_vibration_mode12.gif|thumb|One of the possible modes of vibration of an idealized circular drum head. These modes are eigenfunctions of a linear operator on a function space, a common construction in functional analysis.]]'''Functional analysis''' is a branch of [[Mathematical analysis (nonfiction)|mathematical analysis]], which studies the [[Transformation (function)|transformations]] of [[Function (nonfiction)|functions]] and their algebraic and topological properties. The field builds upon and abstracts the results of [[Joseph Fourier (nonfiction)|Joseph Fourier]]'s 1822 paper, ''Théorie analytique de la chaleur'' (The Analytical Theory of Heat), which demonstrated how a change of basis by means of the Fourier transform could be used to permit manipulations of a function in the frequency domain to obtain insights that were previously unobtainable. Functional analysis has modern applications in many areas of algebra, in particular associative algebra, in probability, operator theory, wavelets and wavelet transforms. The functional data analysis (FDA) paradigm of James O. Ramsay and Bernard Silverman ties functional analysis into principal component analysis and dimensionality reduction. | ||
Functional analysis has strong parallels with linear algebra, as both fields are based on vector spaces as the core algebraic structure. Functional analysis endows linear algebra with concepts from topology (e.g. inner product, norm, topological space) in defining the topological vector space (TVS)[speculation?], which strengthens notions of continuity and limit, and supports generalization to infinite-dimensional spaces. The core operation within a TVS is linear transformation. | |||
An important part of functional analysis is the extension of the theory of measure, integration, and probability to infinite dimensional spaces, also known as infinite dimensional analysis. Additionally, functional analysis generalizes the concept of an orthonormal basis—as found in Fourier analysis—to arbitrary inner product spaces, including those of infinite dimension. Important theoretical results include the Banach–Steinhaus theorem, spectral theorem (central to operator theory), Hahn–Banach theorem, open mapping theorem, and closed graph theorem. | |||
The historical roots of functional analysis lie in the study of spaces of functions and the formulation of properties of transformations of functions such as the Fourier transform as transformations defining continuous, unitary etc. operators between function spaces. This point of view turned out to be particularly useful for the study of differential and integral equations. | |||
The usage of the word functional as a noun goes back to the calculus of variations, implying a function whose argument is a function. The term was first used in Leçons sur le calcul des variations (1910) by Jacques Hadamard. However, the general concept of a functional had previously been introduced in 1887 by the Italian mathematician and physicist [[Vito Volterra (nonfiction)|Vito Volterra]]. The theory of nonlinear functionals was continued by students of Hadamard, in particular Maurice René Fréchet and Paul Lévy. Hadamard also founded the modern school of linear functional analysis further developed by Frigyes Riesz and the Polish Lwów School of Mathematics centered around [[Stefan Banach (nonfiction)|Stefan Banach]]. | |||
== In the News == | == In the News == | ||
Latest revision as of 03:49, 30 November 2020
Functional analysis is a branch of mathematical analysis, which studies the transformations of functions and their algebraic and topological properties. The field builds upon and abstracts the results of Joseph Fourier's 1822 paper, Théorie analytique de la chaleur (The Analytical Theory of Heat), which demonstrated how a change of basis by means of the Fourier transform could be used to permit manipulations of a function in the frequency domain to obtain insights that were previously unobtainable. Functional analysis has modern applications in many areas of algebra, in particular associative algebra, in probability, operator theory, wavelets and wavelet transforms. The functional data analysis (FDA) paradigm of James O. Ramsay and Bernard Silverman ties functional analysis into principal component analysis and dimensionality reduction.
Functional analysis has strong parallels with linear algebra, as both fields are based on vector spaces as the core algebraic structure. Functional analysis endows linear algebra with concepts from topology (e.g. inner product, norm, topological space) in defining the topological vector space (TVS)[speculation?], which strengthens notions of continuity and limit, and supports generalization to infinite-dimensional spaces. The core operation within a TVS is linear transformation.
An important part of functional analysis is the extension of the theory of measure, integration, and probability to infinite dimensional spaces, also known as infinite dimensional analysis. Additionally, functional analysis generalizes the concept of an orthonormal basis—as found in Fourier analysis—to arbitrary inner product spaces, including those of infinite dimension. Important theoretical results include the Banach–Steinhaus theorem, spectral theorem (central to operator theory), Hahn–Banach theorem, open mapping theorem, and closed graph theorem.
The historical roots of functional analysis lie in the study of spaces of functions and the formulation of properties of transformations of functions such as the Fourier transform as transformations defining continuous, unitary etc. operators between function spaces. This point of view turned out to be particularly useful for the study of differential and integral equations.
The usage of the word functional as a noun goes back to the calculus of variations, implying a function whose argument is a function. The term was first used in Leçons sur le calcul des variations (1910) by Jacques Hadamard. However, the general concept of a functional had previously been introduced in 1887 by the Italian mathematician and physicist Vito Volterra. The theory of nonlinear functionals was continued by students of Hadamard, in particular Maurice René Fréchet and Paul Lévy. Hadamard also founded the modern school of linear functional analysis further developed by Frigyes Riesz and the Polish Lwów School of Mathematics centered around Stefan Banach.
In the News
Fiction cross-reference
Nonfiction cross-reference
External links
- Functional analysis @ Wikipedia