Binomial theorem (nonfiction): Difference between revisions
Jump to navigation
Jump to search
No edit summary |
No edit summary |
||
| Line 1: | Line 1: | ||
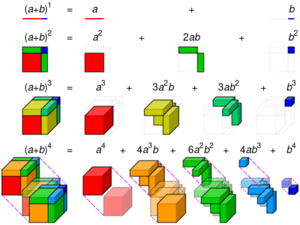
In [[Elementary algebra (nonfiction)|elementary algebra]], the '''binomial theorem''' (or binomial expansion) describes the algebraic expansion of powers of a binomial. According to the theorem, it is possible to expand the polynomial (x + y)n into a sum involving terms of the form axbyc, where the exponents b and c are nonnegative integers with b + c = n, and the coefficient a of each term is a specific positive integer depending on n and b. | [[File:Binomial theorem visualization.svg|thumb|Visualization of binomial expansion up to the 4th power.]]In [[Elementary algebra (nonfiction)|elementary algebra]], the '''binomial theorem''' (or binomial expansion) describes the algebraic expansion of powers of a binomial. According to the theorem, it is possible to expand the polynomial (x + y)n into a sum involving terms of the form axbyc, where the exponents b and c are nonnegative integers with b + c = n, and the coefficient a of each term is a specific positive integer depending on n and b. | ||
== In the News == | |||
<gallery> | |||
</gallery> | |||
== Fiction cross-reference == | |||
* [[Crimes against mathematical constants]] | |||
* [[Gnomon algorithm]] | |||
* [[Gnomon Chronicles]] | |||
* [[Mathematics]] | |||
== Nonfiction cross-reference == | |||
* [[Mathematics (nonfiction)]] | |||
* [[Elementary algebra (nonfiction)]] | |||
== External links == | |||
* [https://en.wikipedia.org/wiki/Binomial_theorem Binomial theorem] @ Wikipedia | |||
[[Category:Nonfiction (nonfiction)]] | |||
[[Category:Mathematics (nonfiction)]] | |||
[[Category:Math needed (nonfiction)]] | |||
Revision as of 06:28, 19 April 2020
In elementary algebra, the binomial theorem (or binomial expansion) describes the algebraic expansion of powers of a binomial. According to the theorem, it is possible to expand the polynomial (x + y)n into a sum involving terms of the form axbyc, where the exponents b and c are nonnegative integers with b + c = n, and the coefficient a of each term is a specific positive integer depending on n and b.
In the News
Fiction cross-reference
Nonfiction cross-reference
External links
- Binomial theorem @ Wikipedia