Riemann hypothesis (nonfiction): Difference between revisions
(Created page with "In mathematics, the '''Riemann hypothesis''' is a conjecture that the Riemann zeta function has its zeros only at the negative even integers and complex numbers with real part...") |
No edit summary |
||
| Line 1: | Line 1: | ||
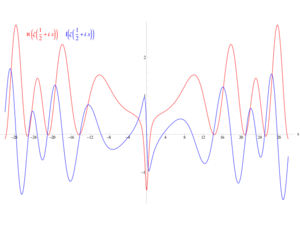
In mathematics, the '''Riemann hypothesis''' is a conjecture that the Riemann zeta function has its zeros only at the negative even integers and complex numbers with real part | [[File:Riemann_critical_line.png|thumb|The real part (red) and imaginary part (blue) of the Riemann zeta function along the critical line Re(s) = 1/2. The first non-trivial zeros can be seen at Im(s) = ±14.135, ±21.022 and ±25.011.]]In [[Mathematics (nonfiction)|mathematics]], the '''Riemann hypothesis''' is a conjecture that the Riemann zeta function has its zeros only at the negative even integers and complex numbers with real part | ||
1 | 1 | ||
/ | / | ||
| Line 25: | Line 25: | ||
/ | / | ||
2 | 2 | ||
+ i t, where t is a real number and i is the imaginary unit. | |||
There are several nontechnical books on the Riemann hypothesis, such as Derbyshire (2003), Rockmore (2005), (Sabbagh 2003a, 2003b), du Sautoy (2003). The books Edwards (1974), Patterson (1988), Borwein et al. (2008) and Mazur & Stein (2015) give mathematical introductions, while Titchmarsh (1986), Ivić (1985) and Karatsuba & Voronin (1992) are advanced monographs. The book Open Problems in Mathematics, edited by John Forbes Nash Jr. and Michael Th. Rassias, features an extensive essay on the Riemann hypothesis by Alain Connes. | There are several nontechnical books on the Riemann hypothesis, such as Derbyshire (2003), Rockmore (2005), (Sabbagh 2003a, 2003b), du Sautoy (2003). The books Edwards (1974), Patterson (1988), Borwein et al. (2008) and Mazur & Stein (2015) give mathematical introductions, while Titchmarsh (1986), Ivić (1985) and Karatsuba & Voronin (1992) are advanced monographs. The book Open Problems in Mathematics, edited by John Forbes Nash Jr. and Michael Th. Rassias, features an extensive essay on the Riemann hypothesis by Alain Connes. | ||
| Line 45: | Line 45: | ||
* [https://en.wikipedia.org/wiki/Riemann_hypothesis Riemann hypothesis] @ Wikipedia | * [https://en.wikipedia.org/wiki/Riemann_hypothesis Riemann hypothesis] @ Wikipedia | ||
[[Category:Nonfiction (nonfiction)]] | [[Category:Nonfiction (nonfiction)]] | ||
[[Category:Mathematics (nonfiction)]] | [[Category:Mathematics (nonfiction)]] | ||
Revision as of 17:07, 24 July 2017
In mathematics, the Riemann hypothesis is a conjecture that the Riemann zeta function has its zeros only at the negative even integers and complex numbers with real part
1 / 2 .
It was proposed by Bernhard Riemann (1859), after whom it is named. The name is also used for some closely related analogues, such as the Riemann hypothesis for curves over finite fields.
The Riemann hypothesis implies results about the distribution of prime numbers.
Along with suitable generalizations, some mathematicians consider it the most important unresolved problem in pure mathematics.
The Riemann hypothesis, along with Goldbach's conjecture, is part of Hilbert's eighth problem in David Hilbert's list of 23 unsolved problems; it is also one of the Clay Mathematics Institute's Millennium Prize Problems.
The Riemann zeta function ζ(s) is a function whose argument s may be any complex number other than 1, and whose values are also complex. It has zeros at the negative even integers; that is, ζ(s) = 0 when s is one of −2, −4, −6, .... These are called its trivial zeros. However, the negative even integers are not the only values for which the zeta function is zero. The other ones are called non-trivial zeros. The Riemann hypothesis is concerned with the locations of these non-trivial zeros, and states that:
The real part of every non-trivial zero of the Riemann zeta function is 1 / 2 .
Thus, if the hypothesis is correct, all the non-trivial zeros lie on the critical line consisting of the complex numbers 1 / 2 + i t, where t is a real number and i is the imaginary unit.
There are several nontechnical books on the Riemann hypothesis, such as Derbyshire (2003), Rockmore (2005), (Sabbagh 2003a, 2003b), du Sautoy (2003). The books Edwards (1974), Patterson (1988), Borwein et al. (2008) and Mazur & Stein (2015) give mathematical introductions, while Titchmarsh (1986), Ivić (1985) and Karatsuba & Voronin (1992) are advanced monographs. The book Open Problems in Mathematics, edited by John Forbes Nash Jr. and Michael Th. Rassias, features an extensive essay on the Riemann hypothesis by Alain Connes.
In the News
Fiction cross-reference
Nonfiction cross-reference
External links:
- Riemann hypothesis @ Wikipedia