Outlier (nonfiction): Difference between revisions
No edit summary |
No edit summary |
||
| Line 1: | Line 1: | ||
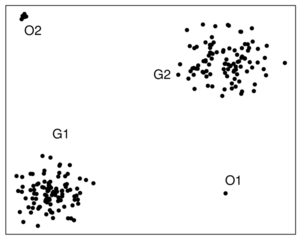
[[File:Two-dimensional_Outliers_Example.png|thumb|Example of two-dimensional outliers. Point labeled O1 and points labeled O2 deviate significantly from regions labeled G1 and G2.]]In | [[File:Two-dimensional_Outliers_Example.png|thumb|Example of two-dimensional outliers. Point labeled O1 and points labeled O2 deviate significantly from regions labeled G1 and G2.]]In statistics, an '''outlier''' is an observation point that is distant from other observations. | ||
== Description == | == Description == | ||
Revision as of 19:12, 7 June 2016
In statistics, an outlier is an observation point that is distant from other observations.
Description
An outlier may be due to variability in the measurement or it may indicate experimental error; the latter are sometimes excluded from the data set.
Outliers can occur by chance in any distribution, but they often indicate either measurement error or that the population has a heavy-tailed distribution.
In most larger samplings of data, some data points will be further away from the sample mean than what is deemed reasonable. This can be due to incidental systematic error or flaws in the theory that generated an assumed family of probability distributions, or it may be that some observations are far from the center of the data. Outlier points can therefore indicate faulty data, erroneous procedures, or areas where a certain theory might not be valid. However, in large samples, a small number of outliers is to be expected (and not due to any anomalous condition).
Naive interpretation
Naive interpretation of statistics derived from data sets that include outliers may be misleading.
For example, if one is calculating the average temperature of 10 objects in a room, and nine of them are between 20 and 25 degrees Celsius, but an oven is at 175 °C, the median of the data will be between 20 and 25 °C but the mean temperature will be between 35.5 and 40 °C.
In this case, the median better reflects the temperature of a randomly sampled object than the mean; naively interpreting the mean as "a typical sample", equivalent to the median, is incorrect.
As illustrated in this case, outliers may indicate data points that belong to a different population than the rest of the sample set.
Robustness
Estimators capable of coping with outliers are said to be robust: the median is a robust statistic, while the mean is not.
Nonfiction cross-reference
Fiction cross-reference
External links
- Outlier @ Wikipedia