Voronoi diagram (nonfiction)

Approximate Voronoi diagram of a set of points. Notice the blended colors in the fuzzy boundary of the Voronoi cells.

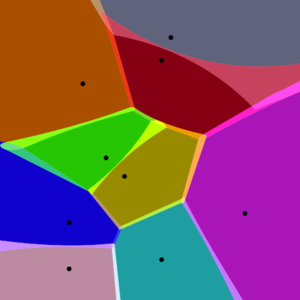
In mathematics, a Voronoi diagram is a partitioning of a plane into regions based on distance to points in a specific subset of the plane.

It is named after Georgy Voronoi, and is also called a Voronoi tessellation, a Voronoi decomposition, a Voronoi partition, or a Dirichlet tessellation (after Peter Gustav Lejeune Dirichlet).

Voronoi diagrams have practical and theoretical applications to a large number of fields, mainly in science and technology but also including visual art.

In the News

• 

  Fantasy Voronoi diagram color commentators discussing recent scores from hotly contested Voronoi diagrams.

Fiction cross-reference

• Fantasy Voronoi diagram
• Mathematics

Nonfiction cross-reference

• Centroidal Voronoi tessellation (nonfiction)
• Lloyd's algorithm (nonfiction)
• Mathematics (nonfiction)
• Mathematical diagram (nonfiction)

External links:

• Voronoi diagram @ Wikipedia

• Very nice Voronoi

• Jump Flood Voronoi for WebGL
  • Online demo
• Voronoi Tessellation
• Voronoi Tesselation - Paper.js
• Voronator - upload 3D model, download your voroni tesselated version
• Voronoi experiment @ karljones.com
• Fortune's algorithm for Voronoi diagrams
• Javascript implementation of Steven J. Fortune's algorithm to compute Voronoi diagrams
• Lloyd’s Relaxation - generates a centroidal Voronoi tessellation, which is where the seed point for each Voronoi region is also its centroid
• Voronoi diagram in JavaScript
• Spherical Voronoi Diagram

• Voronoi diagram code examples @ rosettacode.org

• Robot Path Planning Using Generalized Voronoi Diagrams