Function (nonfiction): Difference between revisions
m (Admin moved page Mathematical function (nonfiction) to Function (mathematics) (nonfiction)) |
No edit summary |
||
| Line 1: | Line 1: | ||
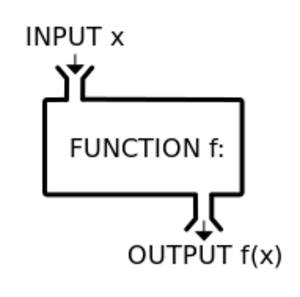
[[File:Mathematical_function.svg|thumb|A function ''f'' takes an input ''x'', and returns a single output ''f(x)''. One metaphor describes the function as a "machine" or "black box" that for each input returns a corresponding output.]]In [[Mathematics (nonfiction)|mathematics]], a '''function''' is a relation between a set of inputs and a set of permissible outputs with the property that each input is related to exactly one [[Output (nonfiction)|output]]. | [[File:Mathematical_function.svg|thumb|A function ''f'' takes an input ''x'', and returns a single output ''f(x)''. One metaphor describes the function as a "machine" or "black box" that for each input returns a corresponding output.]]In [[Mathematics (nonfiction)|mathematics]], a '''function''' is a relation between a set of inputs and a set of permissible outputs with the property that each input is related to exactly one [[Output (nonfiction)|output]]. | ||
An example is the function that relates each real number x to its square x2. | An example is the function that relates each [[Real number (nonfiction)|real number]] x to its square x2. | ||
The output of a function f corresponding to an input x is denoted by f(x) (read "f of x"). | The output of a function f corresponding to an input x is denoted by f(x) (read "f of x"). | ||
Revision as of 17:04, 22 November 2017
In mathematics, a function is a relation between a set of inputs and a set of permissible outputs with the property that each input is related to exactly one output.
An example is the function that relates each real number x to its square x2.
The output of a function f corresponding to an input x is denoted by f(x) (read "f of x").
In this example, if the input is −3, then the output is 9, and we may write f(−3) = 9.
Likewise, if the input is 3, then the output is also 9, and we may write f(3) = 9. (The same output may be produced by more than one input, but each input gives only one output.)
In the News
Supervillains Forbidden Ratio and Gnotilus form crime team to destroy the Golden ratio.
Halting problem is delicious, says supervillain Forbidden Ratio.
Asclepius Myrmidon finds Halting problem, forecasts multiple casualties from Pi disaster.
Fiction cross-reference
- Asclepius Myrmidon
- Forbidden Ratio - a mathematical function and supervillain.
- Killer Poke - a software defect for hire, and contract killer for Murder, Incorporated 1.1.
- Pi disaster
Nonfiction cross-reference
External links:
- Function (mathematics) @ Wikipedia