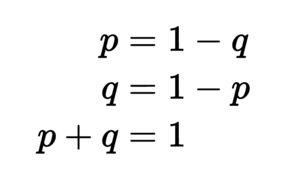Bernoulli trial (nonfiction): Difference between revisions
(Created page with "In the theory of probability and statistics, a '''Bernoulli trial''' (or '''binomial trial''') is a random experiment with exactly two possible outcomes, "success" and "failur...") |
No edit summary |
||
| Line 1: | Line 1: | ||
In the theory of probability and statistics, a '''Bernoulli trial''' (or '''binomial trial''') is a random experiment with exactly two possible outcomes, "success" and "failure", in which the probability of success is the same every time the experiment is conducted. It is named after [[Jacob Bernoulli (nonfiction)|Jacob Bernoulli]], a 17th century Swiss mathematician. | [[File:Bernoulli_trial.png|thumb|Simple equation representing a Bernoulli trial.]]In the theory of probability and statistics, a '''Bernoulli trial''' (or '''binomial trial''') is a random experiment with exactly two possible outcomes, "success" and "failure", in which the probability of success is the same every time the experiment is conducted. It is named after [[Jacob Bernoulli (nonfiction)|Jacob Bernoulli]], a 17th century Swiss mathematician. | ||
Since a Bernoulli trial has only two possible outcomes, it can be framed as some "yes or no" question. For example: | Since a Bernoulli trial has only two possible outcomes, it can be framed as some "yes or no" question. For example: | ||
Latest revision as of 10:05, 14 April 2017
In the theory of probability and statistics, a Bernoulli trial (or binomial trial) is a random experiment with exactly two possible outcomes, "success" and "failure", in which the probability of success is the same every time the experiment is conducted. It is named after Jacob Bernoulli, a 17th century Swiss mathematician.
Since a Bernoulli trial has only two possible outcomes, it can be framed as some "yes or no" question. For example:
- Is the top card of a shuffled deck an ace?
- Did a flipped coin land face up?
Therefore, success and failure are merely labels for the two outcomes, and should not be construed literally. The term "success" in this sense consists in the result meeting specified conditions, not in any moral judgement. More generally, given any probability space, for any event (set of outcomes), one can define a Bernoulli trial, corresponding to whether the event occurred or not (event or complementary event).
Examples of Bernoulli trials include:
- Flipping a coin. In this context, obverse ("heads") conventionally denotes success and reverse ("tails") denotes failure. A fair coin has the probability of success 0.5 by definition. In this case there are exactly two outcomes.
- Rolling a dice, where a six is "success" and everything else a "failure". In this case there are six outcomes, and the event is a six; the complementary event "not a six" corresponds to the other five outcomes.
- In conducting a political opinion poll, choosing a voter at random to ascertain whether that voter will vote "yes" in an upcoming referendum.
The mathematical formalisation of the Bernoulli trial is known as the Bernoulli process. This article offers an elementary introduction to the concept, whereas the article on the Bernoulli process offers a more advanced treatment.
In the News
Fiction cross-reference
Nonfiction cross-reference
External links:
- Bernoulli trial @ Wikipedia