Voronoi diagram (nonfiction): Difference between revisions
Jump to navigation
Jump to search
No edit summary |
No edit summary |
||
| (5 intermediate revisions by the same user not shown) | |||
| Line 13: | Line 13: | ||
== Fiction cross-reference == | == Fiction cross-reference == | ||
* [[Gnomon algorithm]] | |||
* [[Gnomon Chronicles]] | |||
* [[Fantasy Voronoi diagram]] | * [[Fantasy Voronoi diagram]] | ||
* [[Mathematics]] | * [[Mathematics]] | ||
* [[Voronoia]] - a pathological mental condition characterized by delusions of Voronoi diagrams. | |||
== Nonfiction cross-reference == | == Nonfiction cross-reference == | ||
* [[Centroidal Voronoi tessellation (nonfiction)]] | |||
* [[Delaunay triangulation (nonfiction)]] - a triangulation DT(P) such that no point in P is inside the circumcircle of any triangle in DT(P). Delaunay triangulations maximize the minimum angle of all the angles of the triangles in the triangulation; they tend to avoid sliver triangles. | |||
* [[Lloyd's algorithm (nonfiction)]] | |||
* [[Mathematics (nonfiction)]] | * [[Mathematics (nonfiction)]] | ||
* [[Mathematical diagram (nonfiction)]] | * [[Mathematical diagram (nonfiction)]] | ||
* [[Wigner–Seitz cell (nonfiction)]] - a [[Primitive cell (nonfiction)|primitive cell]] which has been constructed by applying Voronoi decomposition to a crystal lattice. It is used in the study of crystalline materials in solid-state physics. | |||
External links: | External links: | ||
| Line 34: | Line 41: | ||
* [http://karljones.com/voronoi/ Voronoi experiment] @ karljones.com | * [http://karljones.com/voronoi/ Voronoi experiment] @ karljones.com | ||
* [https://www.desmos.com/calculator/ejatebvup4 Fortune's algorithm for Voronoi diagrams] | * [https://www.desmos.com/calculator/ejatebvup4 Fortune's algorithm for Voronoi diagrams] | ||
* [http://www.raymondhill.net/voronoi/rhill-voronoi.html Javascript implementation of Steven J. Fortune's algorithm to compute Voronoi diagrams] | |||
* [https://www.jasondavies.com/lloyd/ Lloyd’s Relaxation] - generates a centroidal Voronoi tessellation, which is where the seed point for each Voronoi region is also its centroid | |||
* [http://blog.ivank.net/voronoi-diagram-in-javascript.html Voronoi diagram in JavaScript] | |||
* [https://www.jasondavies.com/maps/voronoi/ Spherical Voronoi Diagram] | |||
* [http://alexbeutel.com/webgl/voronoi.html Interactive Voronoi Diagram Generator with WebGL] | |||
* [https://rosettacode.org/wiki/Voronoi_diagram Voronoi diagram code examples] @ rosettacode.org | * [https://rosettacode.org/wiki/Voronoi_diagram Voronoi diagram code examples] @ rosettacode.org | ||
Latest revision as of 04:33, 9 February 2020
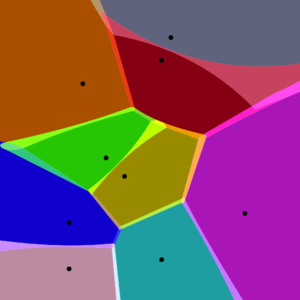
In mathematics, a Voronoi diagram is a partitioning of a plane into regions based on distance to points in a specific subset of the plane.
It is named after Georgy Voronoi, and is also called a Voronoi tessellation, a Voronoi decomposition, a Voronoi partition, or a Dirichlet tessellation (after Peter Gustav Lejeune Dirichlet).
Voronoi diagrams have practical and theoretical applications to a large number of fields, mainly in science and technology but also including visual art.
In the News
Fantasy Voronoi diagram color commentators discussing recent scores from hotly contested Voronoi diagrams.
Fiction cross-reference
- Gnomon algorithm
- Gnomon Chronicles
- Fantasy Voronoi diagram
- Mathematics
- Voronoia - a pathological mental condition characterized by delusions of Voronoi diagrams.
Nonfiction cross-reference
- Centroidal Voronoi tessellation (nonfiction)
- Delaunay triangulation (nonfiction) - a triangulation DT(P) such that no point in P is inside the circumcircle of any triangle in DT(P). Delaunay triangulations maximize the minimum angle of all the angles of the triangles in the triangulation; they tend to avoid sliver triangles.
- Lloyd's algorithm (nonfiction)
- Mathematics (nonfiction)
- Mathematical diagram (nonfiction)
- Wigner–Seitz cell (nonfiction) - a primitive cell which has been constructed by applying Voronoi decomposition to a crystal lattice. It is used in the study of crystalline materials in solid-state physics.
External links:
- Voronoi diagram @ Wikipedia
- Jump Flood Voronoi for WebGL
- Voronoi Tessellation
- Voronoi Tesselation - Paper.js
- Voronator - upload 3D model, download your voroni tesselated version
- Voronoi experiment @ karljones.com
- Fortune's algorithm for Voronoi diagrams
- Javascript implementation of Steven J. Fortune's algorithm to compute Voronoi diagrams
- Lloyd’s Relaxation - generates a centroidal Voronoi tessellation, which is where the seed point for each Voronoi region is also its centroid
- Voronoi diagram in JavaScript
- Spherical Voronoi Diagram
- Interactive Voronoi Diagram Generator with WebGL
- Voronoi diagram code examples @ rosettacode.org