Blossom algorithm (nonfiction): Difference between revisions
(Created page with "The '''blossom algorithm''' is an algorithm in graph theory for constructing maximum matchings on graphs. The algorith...") |
No edit summary |
||
| Line 1: | Line 1: | ||
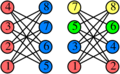
The '''blossom algorithm''' is an [[Algorithm (nonfiction)|algorithm]] in [[Graph theory (nonfiction)|graph theory]] for constructing maximum matchings on graphs. The algorithm was developed by Jack Edmonds in 1961, and published in 1965. Given a general graph G = (V, E), the algorithm finds a matching M such that each vertex in V is incident with at most one edge in M and |M| is maximized. The matching is constructed by iteratively improving an initial empty matching along augmenting paths in the graph. Unlike bipartite matching, the key new idea is that an odd-length cycle in the graph (blossom) is contracted to a single vertex, with the search continuing iteratively in the contracted graph. | [[File:Blossom_with_Edmonds_matching_algorithm.svg|thumb|]]The '''blossom algorithm''' is an [[Algorithm (nonfiction)|algorithm]] in [[Graph theory (nonfiction)|graph theory]] for constructing maximum matchings on graphs. The algorithm was developed by Jack Edmonds in 1961, and published in 1965. Given a general graph G = (V, E), the algorithm finds a matching M such that each vertex in V is incident with at most one edge in M and |M| is maximized. The matching is constructed by iteratively improving an initial empty matching along augmenting paths in the graph. Unlike bipartite matching, the key new idea is that an odd-length cycle in the graph (blossom) is contracted to a single vertex, with the search continuing iteratively in the contracted graph. | ||
A major reason that the blossom algorithm is important is that it gave the first proof that a maximum-size matching could be found using a polynomial amount of computation time. Another reason is that it led to a linear programming polyhedral description of the matching polytope, yielding an algorithm for min-weight matching. As elaborated by Alexander Schrijver, further significance of the result comes from the fact that this was the first polytope whose proof of integrality "does not simply follow just from total unimodularity, and its description was a breakthrough in polyhedral combinatorics." | A major reason that the blossom algorithm is important is that it gave the first proof that a maximum-size matching could be found using a polynomial amount of computation time. Another reason is that it led to a linear programming polyhedral description of the matching polytope, yielding an algorithm for min-weight matching. As elaborated by Alexander Schrijver, further significance of the result comes from the fact that this was the first polytope whose proof of integrality "does not simply follow just from total unimodularity, and its description was a breakthrough in polyhedral combinatorics." | ||
== In the News == | |||
<gallery> | |||
File:Greedy colorings.svg|link=Greedy coloring (nonfiction)|September 4, 1973: An experimental graph coloring model accidentally generates a [[Greedy coloring (nonfiction)|Greedy coloring]] computer virus which causes the color [[Green (nonfiction)|green]] to become [[Red (nonfiction)|red]] in the vicinity of every computer terminal around the world. The virus will be eliminated several hours later by [[Algorithmic Paradigm Treaty Organization|APTO]] troubleshooters, restoring [[Green (nonfiction)|green]] to its normal appearance. | |||
</gallery> | |||
== Fiction cross-reference == | |||
* [[Crimes against mathematical constants]] | |||
* [[Gnomon algorithm]] | |||
* [[Gnomon Chronicles]] | |||
* [[Mathematics]] | |||
== Nonfiction cross-reference == | |||
* [[Discrete mathematics (nonfiction)]] | |||
* [[Graph theory (nonfiction)]] | |||
* [[Mathematics (nonfiction)]] | |||
Related categories: | |||
* [[:Category:Graph theorists (nonfiction)]] | |||
External links: | |||
* [https://en.wikipedia.org/wiki/Blossom_algorithm Blossom algorithm] @ Wikipedia | |||
[[Category:Nonfiction (nonfiction)]] | |||
[[Category:Graph theory (nonfiction)]] | |||
[[Category:Mathematics (nonfiction)]] | |||
Latest revision as of 12:25, 3 September 2018
The blossom algorithm is an algorithm in graph theory for constructing maximum matchings on graphs. The algorithm was developed by Jack Edmonds in 1961, and published in 1965. Given a general graph G = (V, E), the algorithm finds a matching M such that each vertex in V is incident with at most one edge in M and |M| is maximized. The matching is constructed by iteratively improving an initial empty matching along augmenting paths in the graph. Unlike bipartite matching, the key new idea is that an odd-length cycle in the graph (blossom) is contracted to a single vertex, with the search continuing iteratively in the contracted graph.
A major reason that the blossom algorithm is important is that it gave the first proof that a maximum-size matching could be found using a polynomial amount of computation time. Another reason is that it led to a linear programming polyhedral description of the matching polytope, yielding an algorithm for min-weight matching. As elaborated by Alexander Schrijver, further significance of the result comes from the fact that this was the first polytope whose proof of integrality "does not simply follow just from total unimodularity, and its description was a breakthrough in polyhedral combinatorics."
In the News
September 4, 1973: An experimental graph coloring model accidentally generates a Greedy coloring computer virus which causes the color green to become red in the vicinity of every computer terminal around the world. The virus will be eliminated several hours later by APTO troubleshooters, restoring green to its normal appearance.
Fiction cross-reference
Nonfiction cross-reference
Related categories:
External links:
- Blossom algorithm @ Wikipedia