Natural number (nonfiction): Difference between revisions
| (3 intermediate revisions by the same user not shown) | |||
| Line 7: | Line 7: | ||
The natural numbers are the basis from which many other number sets may be built by extension: | The natural numbers are the basis from which many other number sets may be built by extension: | ||
* The integers, by including (if not yet in) the neutral element 0 and an additive inverse (−n) for each nonzero natural number n | * The [[Integer (nonfiction)|integers]], by including (if not yet in) the neutral element 0 and an additive inverse (−n) for each nonzero natural number n | ||
* The rational numbers, by including a multiplicative inverse (1/n) for each nonzero integer n (and also the product of these inverses by integers) | * The [[Rational number (nonfiction)|rational numbers]], by including a multiplicative inverse (1/''n'') for each nonzero integer ''n'' (and also the product of these inverses by integers) | ||
* The real numbers by including with the rationals the limits of (converging) Cauchy sequences of rationals | * The real numbers by including with the rationals the limits of (converging) Cauchy sequences of rationals | ||
* The complex numbers, by including with the real numbers the unresolved square root of minus one (and also the sums and products of thereof) | * The complex numbers, by including with the real numbers the unresolved square root of minus one (and also the sums and products of thereof) | ||
| Line 25: | Line 25: | ||
<gallery> | <gallery> | ||
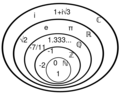
File:Numbers diagram.svg|link=Number (nonfiction)|Diagram of [[Number (nonfiction)|numbers]] says it "loves all numbers equally, despite occasional squabbling between integers and complex numbers." | File:Numbers diagram.svg|link=Number (nonfiction)|Diagram of [[Number (nonfiction)|numbers]] says it "loves all numbers equally, despite occasional squabbling between integers and complex numbers." | ||
File:Zahlen symbol.svg|link=Integer (nonfiction)|New study of [[Integer (nonfiction)|integers]] indicates that they "may be vulnerable to [[crimes against mathematical constants]]." | |||
File:Digits_of_pi.svg|link=Irrational number (nonfiction)|New survey of [[Irrational number (nonfiction)|irrational numbers]] indicates that they "feel intellectually superior to natural numbers." | |||
</gallery> | </gallery> | ||
Latest revision as of 14:04, 14 November 2017
In mathematics, the natural numbers are those numbers used for counting (as in "there are six coins on the table") and ordering (as in "this is the third largest city in the country").
In common language, words used for counting are "cardinal numbers" and words used for ordering are "ordinal numbers".
Some definitions, including the standard ISO 80000-2, begin the natural numbers with 0, corresponding to the non-negative integers 0, 1, 2, 3, …, whereas others start with 1, corresponding to the positive integers 1, 2, 3, …. Texts that exclude zero from the natural numbers sometimes refer to the natural numbers together with zero as the whole numbers, but in other writings, that term is used instead for the integers (including negative integers).
The natural numbers are the basis from which many other number sets may be built by extension:
- The integers, by including (if not yet in) the neutral element 0 and an additive inverse (−n) for each nonzero natural number n
- The rational numbers, by including a multiplicative inverse (1/n) for each nonzero integer n (and also the product of these inverses by integers)
- The real numbers by including with the rationals the limits of (converging) Cauchy sequences of rationals
- The complex numbers, by including with the real numbers the unresolved square root of minus one (and also the sums and products of thereof)
- And so on
These chains of extensions make the natural numbers canonically embedded (identified) in the other number systems.
Properties of the natural numbers, such as divisibility and the distribution of prime numbers, are studied in number theory. Problems concerning counting and ordering, such as partitioning and enumerations, are studied in combinatorics.
In common language, for example in primary school, natural numbers may be called counting numbers both to intuitively exclude the negative integers and zero, and also to contrast the discreteness of counting to the continuity of measurement, established by the real numbers.
The natural numbers can, at times, appear as a convenient set of names (labels), that is, as what linguists call nominal numbers, foregoing many or all of the properties of being a number in a mathematical sense.
In the News
Diagram of numbers says it "loves all numbers equally, despite occasional squabbling between integers and complex numbers."
New study of integers indicates that they "may be vulnerable to crimes against mathematical constants."
New survey of irrational numbers indicates that they "feel intellectually superior to natural numbers."
Fiction cross-reference
Nonfiction cross-reference
External links:
- Natural number @ Wikipedia