Wild knot (nonfiction): Difference between revisions
Jump to navigation
Jump to search
(Created page with "In the mathematical theory of knots, a wild knot is a knot that is not tame. Wild knots can have pathological behavior. A knot is tame if it can be "thickened up" -- that is...") |
No edit summary |
||
| (2 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
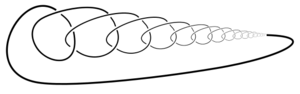
In the mathematical theory of knots, a wild knot is a knot that is not tame. Wild knots can have pathological behavior. | [[File:Wild knot.png|thumb|A wild knot.]]In the mathematical theory of knots, a '''wild knot''' is a knot that is not tame. Wild knots can have pathological behavior. | ||
A knot is tame if it can be "thickened up" -- that is, if there exists an extension to an embedding of the solid torus S 1 × D 2 into the 3-sphere. | A knot is tame if it can be "thickened up" -- that is, if there exists an extension to an embedding of the solid torus S 1 × D 2 into the 3-sphere. | ||
| Line 20: | Line 20: | ||
* [[Crimes against mathematical constants]] | * [[Crimes against mathematical constants]] | ||
* [[Gnomon algorithm]] | * [[Gnomon algorithm]] | ||
* [[Gnomon Chronicles]] | |||
== Nonfiction cross-reference == | == Nonfiction cross-reference == | ||
| Line 26: | Line 27: | ||
* [[Wild arc (nonfiction)]] | * [[Wild arc (nonfiction)]] | ||
External links | == External links == | ||
* [https://twitter.com/GnomonChronicl1/status/1387399730267893762 Post] @ Twitter (28 April 2021) | |||
* [https://en.wikipedia.org/wiki/Wild_knot Wild knot] @ Wikipedia | * [https://en.wikipedia.org/wiki/Wild_knot Wild knot] @ Wikipedia | ||
[[Category:Nonfiction (nonfiction)]] | [[Category:Nonfiction (nonfiction)]] | ||
[[Category:Mathematics (nonfiction)]] | [[Category:Mathematics (nonfiction)]] | ||
[[Category:Topology (nonfiction)]] | |||
Latest revision as of 14:39, 22 November 2021
In the mathematical theory of knots, a wild knot is a knot that is not tame. Wild knots can have pathological behavior.
A knot is tame if it can be "thickened up" -- that is, if there exists an extension to an embedding of the solid torus S 1 × D 2 into the 3-sphere.
A knot is tame if and only if it can be represented as a finite closed polygonal chain.
Smooth knots, for example, are always tame.
In knot theory and 3-manifold theory, often the adjective "tame" is omitted.
Wild knots can be found in some Celtic designs.