Forbidden graph characterization (nonfiction): Difference between revisions
(Created page with "In graph theory, a branch of mathematics, a '''forbidden graph characterization''' is a method of specifying a family of graph, or hypergraph, str...") |
No edit summary |
||
| (7 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
[[File:Forbidden_indifference_subgraphs.png|thumb|Forbidden induced subgraphs for the [[Indifference graph (nonfiction)|indifference graphs]]: the claw, sun, and net (top, left–right) and cycles of length four or more (bottom).]]In [[Graph theory (nonfiction)|graph theory]], a '''forbidden graph characterization''' is a method of specifying a family of graph, or hypergraph, structures, by specifying substructures that are forbidden from existing within any graph in the family. | |||
Different families vary in the nature of what is forbidden. In general, a structure G is a member of a family F if and only if a forbidden substructure is not contained in G. The forbidden substructure might be one of: | Different families vary in the nature of what is forbidden. In general, a structure G is a member of a family F if and only if a forbidden substructure is not contained in G. The forbidden substructure might be one of: | ||
| Line 10: | Line 10: | ||
The set of structures that are forbidden from belonging to a given graph family can also be called an obstruction set for that family. | The set of structures that are forbidden from belonging to a given graph family can also be called an obstruction set for that family. | ||
Forbidden graph characterizations may be used in algorithms for testing whether a graph belongs to a given family. In many cases, it is possible to test in polynomial time whether a given graph contains any of the members of the obstruction set, and therefore whether it belongs to the family defined by that obstruction set. | Forbidden graph characterizations may be used in [[Algorithm (nonfiction)|algorithms]] for testing whether a graph belongs to a given family. In many cases, it is possible to test in polynomial time whether a given graph contains any of the members of the obstruction set, and therefore whether it belongs to the family defined by that obstruction set. | ||
In order for a family to have a forbidden graph characterization, with a particular type of substructure, the family must be closed under substructures. That is, every substructure (of a given type) of a graph in the family must be another graph in the family. Equivalently, if a graph is not part of the family, all larger graphs containing it as a substructure must also be excluded from the family. When this is true, there always exists an obstruction set (the set of graphs that are not in the family but whose smaller substructures all belong to the family). However, for some notions of what a substructure is, this obstruction set could be infinite. The Robertson–Seymour theorem proves that, for the particular case of graph minors, a family that is closed under minors always has a finite obstruction set. | In order for a family to have a forbidden graph characterization, with a particular type of substructure, the family must be closed under substructures. That is, every substructure (of a given type) of a graph in the family must be another graph in the family. Equivalently, if a graph is not part of the family, all larger graphs containing it as a substructure must also be excluded from the family. When this is true, there always exists an obstruction set (the set of graphs that are not in the family but whose smaller substructures all belong to the family). However, for some notions of what a substructure is, this obstruction set could be infinite. The Robertson–Seymour theorem proves that, for the particular case of graph minors, a family that is closed under minors always has a finite obstruction set. | ||
| Line 17: | Line 17: | ||
<gallery> | <gallery> | ||
File:Anarchimedes constructing Lego solar system.jpg|link=Anarchimedes|Evidence emerges that rogue mathematician and alleged time-traveler '''[[Anarchimedes]]''' is constructing a LEGO-powered doomsday weapon. | |||
File:Indifference graph.png|link=Indifference graph (nonfiction)|[[Indifference graph (nonfiction)|Indifference graph]] says it "has nothing to say to forbidden graph characterizations." | |||
</gallery> | </gallery> | ||
== Fiction cross-reference == | == Fiction cross-reference == | ||
* [[Anarchimedes]] | |||
* [[Crimes against mathematical constants]] | |||
* [[Gnomon algorithm]] | |||
* [[Gnomon Chronicles]] | |||
* [[Mathematics (nonfiction)]] | |||
== Nonfiction cross-reference == | == Nonfiction cross-reference == | ||
* [[Indifference graph (nonfiction)]] | |||
* [[Graph theory (nonfiction)]] | |||
* [[Mathematics (nonfiction)]] | * [[Mathematics (nonfiction)]] | ||
* [[Pál Turán (nonfiction)]] | |||
External links | == External links == | ||
* [https://en.wikipedia.org/wiki/Forbidden_graph_characterization Forbidden graph characterization] @ Wikipedia | * [https://en.wikipedia.org/wiki/Forbidden_graph_characterization Forbidden graph characterization] @ Wikipedia | ||
[[Category:Nonfiction (nonfiction)]] | [[Category:Nonfiction (nonfiction)]] | ||
[[Category:Graph theory (nonfiction)]] | |||
[[Category:Mathematics (nonfiction)]] | [[Category:Mathematics (nonfiction)]] | ||
[[Category:Anarchimedes]] | |||
[[Category:Crimes against mathematical constants]] | |||
Latest revision as of 06:23, 3 September 2021
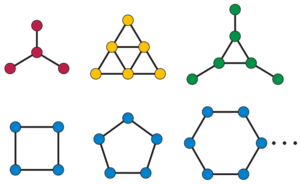
In graph theory, a forbidden graph characterization is a method of specifying a family of graph, or hypergraph, structures, by specifying substructures that are forbidden from existing within any graph in the family.
Different families vary in the nature of what is forbidden. In general, a structure G is a member of a family F if and only if a forbidden substructure is not contained in G. The forbidden substructure might be one of:
- subgraphs, smaller graphs obtained from subsets of the vertices and edges of a larger graph,
induced subgraphs, smaller graphs obtained by selecting a subset of the vertices and using all edges with both endpoints in that subset,
- homeomorphic subgraphs (also called topological minors), smaller graphs obtained from subgraphs by collapsing paths of degree-two vertices to single edges, or
- graph minors, smaller graphs obtained from subgraphs by arbitrary edge contractions.
The set of structures that are forbidden from belonging to a given graph family can also be called an obstruction set for that family.
Forbidden graph characterizations may be used in algorithms for testing whether a graph belongs to a given family. In many cases, it is possible to test in polynomial time whether a given graph contains any of the members of the obstruction set, and therefore whether it belongs to the family defined by that obstruction set.
In order for a family to have a forbidden graph characterization, with a particular type of substructure, the family must be closed under substructures. That is, every substructure (of a given type) of a graph in the family must be another graph in the family. Equivalently, if a graph is not part of the family, all larger graphs containing it as a substructure must also be excluded from the family. When this is true, there always exists an obstruction set (the set of graphs that are not in the family but whose smaller substructures all belong to the family). However, for some notions of what a substructure is, this obstruction set could be infinite. The Robertson–Seymour theorem proves that, for the particular case of graph minors, a family that is closed under minors always has a finite obstruction set.
In the News
Evidence emerges that rogue mathematician and alleged time-traveler Anarchimedes is constructing a LEGO-powered doomsday weapon.
Indifference graph says it "has nothing to say to forbidden graph characterizations."
Fiction cross-reference
- Anarchimedes
- Crimes against mathematical constants
- Gnomon algorithm
- Gnomon Chronicles
- Mathematics (nonfiction)
Nonfiction cross-reference
- Indifference graph (nonfiction)
- Graph theory (nonfiction)
- Mathematics (nonfiction)
- Pál Turán (nonfiction)
External links
- Forbidden graph characterization @ Wikipedia
