Voronoi diagram (nonfiction): Difference between revisions
Jump to navigation
Jump to search
No edit summary |
No edit summary |
||
| Line 1: | Line 1: | ||
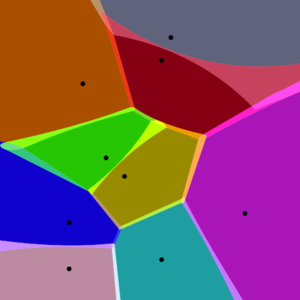
[[File:Approximate Voronoi Diagram.svg.png|thumb|Approximate Voronoi diagram of a set of points. Notice the blended colors in the fuzzy boundary of the Voronoi cells.]]In [[mathematics (nonfiction)]], a '''Voronoi diagram''' is a partitioning of a plane into regions based on distance to points in a specific subset of the plane. | [[File:Approximate Voronoi Diagram.svg.png|thumb|Approximate Voronoi diagram of a set of points. Notice the blended colors in the fuzzy boundary of the Voronoi cells.]]In [[mathematics (nonfiction)]], a '''Voronoi diagram''' is a partitioning of a plane into regions based on distance to points in a specific subset of the plane. | ||
It is named after Georgy Voronoi, and is also called a Voronoi tessellation, a Voronoi decomposition, a Voronoi partition, or a Dirichlet tessellation (after Peter Gustav Lejeune Dirichlet). | It is named after Georgy Voronoi, and is also called a Voronoi tessellation, a Voronoi decomposition, a Voronoi partition, or a Dirichlet tessellation (after Peter Gustav Lejeune Dirichlet). | ||
| Line 13: | Line 5: | ||
Voronoi diagrams have practical and theoretical applications to a large number of fields, mainly in science and technology but also including visual art. | Voronoi diagrams have practical and theoretical applications to a large number of fields, mainly in science and technology but also including visual art. | ||
== | == Fiction cross-reference == | ||
= | <gallery mode="traditional"> | ||
File:Voronoi-diagram-color-commentators.jpg|thumb|[[Color commentators (nonfiction)|Color commentators]] discussing recent scores from hotly contested [[Voronoi diagrams (nonfiction)|Voronoi diagrams]]. | |||
</gallery> | |||
* [[Fantasy Voronoi diagram]] | * [[Fantasy Voronoi diagram]] | ||
== Nonfiction cross-reference == | |||
== External links == | == External links == | ||
Revision as of 10:43, 12 June 2016
In mathematics (nonfiction), a Voronoi diagram is a partitioning of a plane into regions based on distance to points in a specific subset of the plane.
It is named after Georgy Voronoi, and is also called a Voronoi tessellation, a Voronoi decomposition, a Voronoi partition, or a Dirichlet tessellation (after Peter Gustav Lejeune Dirichlet).
Voronoi diagrams have practical and theoretical applications to a large number of fields, mainly in science and technology but also including visual art.
Fiction cross-reference
Color commentators discussing recent scores from hotly contested Voronoi diagrams.
Nonfiction cross-reference
External links
- Voronoi diagram @ wiki.karljones.com
- Voronoi diagram @ Wikipedia