Voronoi diagram (nonfiction): Difference between revisions
From Gnomon Chronicles
No edit summary |
|||
| (14 intermediate revisions by the same user not shown) | |||
| Line 5: | Line 5: | ||
Voronoi diagrams have practical and theoretical applications to a large number of fields, mainly in science and technology but also including visual art. | Voronoi diagrams have practical and theoretical applications to a large number of fields, mainly in science and technology but also including visual art. | ||
== | == In the News == | ||
<gallery | <gallery> | ||
File:Voronoi-diagram-color-commentators.jpg|link=Fantasy Voronoi diagram|[[Fantasy Voronoi diagram]] color commentators discussing recent scores from hotly contested Voronoi diagrams. | File:Voronoi-diagram-color-commentators.jpg|link=Fantasy Voronoi diagram|[[Fantasy Voronoi diagram]] color commentators discussing recent scores from hotly contested Voronoi diagrams. | ||
</gallery> | </gallery> | ||
== Fiction cross-reference == | |||
* [[Gnomon algorithm]] | |||
* [[Gnomon Chronicles]] | |||
* [[Fantasy Voronoi diagram]] | * [[Fantasy Voronoi diagram]] | ||
* [[Mathematics]] | * [[Mathematics]] | ||
* [[Voronoia]] - a pathological mental condition characterized by delusions of Voronoi diagrams. | |||
== Nonfiction cross-reference == | == Nonfiction cross-reference == | ||
* [[Centroidal Voronoi tessellation (nonfiction)]] | |||
* [[Delaunay triangulation (nonfiction)]] - a triangulation DT(P) such that no point in P is inside the circumcircle of any triangle in DT(P). Delaunay triangulations maximize the minimum angle of all the angles of the triangles in the triangulation; they tend to avoid sliver triangles. | |||
* [[Lloyd's algorithm (nonfiction)]] | |||
* [[Mathematics (nonfiction)]] | |||
* [[Mathematical diagram (nonfiction)]] | |||
* [[Wigner–Seitz cell (nonfiction)]] - a [[Primitive cell (nonfiction)|primitive cell]] which has been constructed by applying Voronoi decomposition to a crystal lattice. It is used in the study of crystalline materials in solid-state physics. | |||
External links: | |||
* [https://en.wikipedia.org/wiki/Voronoi_diagram Voronoi diagram] @ Wikipedia | * [https://en.wikipedia.org/wiki/Voronoi_diagram Voronoi diagram] @ Wikipedia | ||
[[Category:Mathematics]] | * [http://creativejs.com/2011/07/voronoi/index.html Very nice Voronoi] | ||
* [http://unitzeroone.com/blog/2011/03/22/jump-flood-voronoi-for-webgl/ Jump Flood Voronoi for WebGL] | |||
** [http://unitzeroone.com/labs/jfavoronoi/ Online demo] | |||
* [https://bl.ocks.org/mbostock/4060366 Voronoi Tessellation] | |||
* [http://paperjs.org/examples/voronoi/ Voronoi Tesselation] - Paper.js | |||
* [https://www.voronator.com/ Voronator] - upload 3D model, download your voroni tesselated version | |||
* [http://karljones.com/voronoi/ Voronoi experiment] @ karljones.com | |||
* [https://www.desmos.com/calculator/ejatebvup4 Fortune's algorithm for Voronoi diagrams] | |||
* [http://www.raymondhill.net/voronoi/rhill-voronoi.html Javascript implementation of Steven J. Fortune's algorithm to compute Voronoi diagrams] | |||
* [https://www.jasondavies.com/lloyd/ Lloyd’s Relaxation] - generates a centroidal Voronoi tessellation, which is where the seed point for each Voronoi region is also its centroid | |||
* [http://blog.ivank.net/voronoi-diagram-in-javascript.html Voronoi diagram in JavaScript] | |||
* [https://www.jasondavies.com/maps/voronoi/ Spherical Voronoi Diagram] | |||
* [http://alexbeutel.com/webgl/voronoi.html Interactive Voronoi Diagram Generator with WebGL] | |||
* [https://rosettacode.org/wiki/Voronoi_diagram Voronoi diagram code examples] @ rosettacode.org | |||
* [https://www.cs.columbia.edu/~pblaer/projects/path_planner/ Robot Path Planning Using Generalized Voronoi Diagrams] | |||
[[Category:Nonfiction (nonfiction)]] | |||
[[Category:Mathematics (nonfiction)]] | |||
Latest revision as of 05:33, 9 February 2020
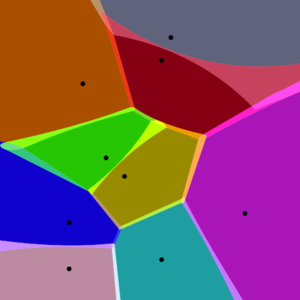
In mathematics, a Voronoi diagram is a partitioning of a plane into regions based on distance to points in a specific subset of the plane.
It is named after Georgy Voronoi, and is also called a Voronoi tessellation, a Voronoi decomposition, a Voronoi partition, or a Dirichlet tessellation (after Peter Gustav Lejeune Dirichlet).
Voronoi diagrams have practical and theoretical applications to a large number of fields, mainly in science and technology but also including visual art.
In the News
Fantasy Voronoi diagram color commentators discussing recent scores from hotly contested Voronoi diagrams.
Fiction cross-reference
- Gnomon algorithm
- Gnomon Chronicles
- Fantasy Voronoi diagram
- Mathematics
- Voronoia - a pathological mental condition characterized by delusions of Voronoi diagrams.
Nonfiction cross-reference
- Centroidal Voronoi tessellation (nonfiction)
- Delaunay triangulation (nonfiction) - a triangulation DT(P) such that no point in P is inside the circumcircle of any triangle in DT(P). Delaunay triangulations maximize the minimum angle of all the angles of the triangles in the triangulation; they tend to avoid sliver triangles.
- Lloyd's algorithm (nonfiction)
- Mathematics (nonfiction)
- Mathematical diagram (nonfiction)
- Wigner–Seitz cell (nonfiction) - a primitive cell which has been constructed by applying Voronoi decomposition to a crystal lattice. It is used in the study of crystalline materials in solid-state physics.
External links:
- Voronoi diagram @ Wikipedia
- Jump Flood Voronoi for WebGL
- Voronoi Tessellation
- Voronoi Tesselation - Paper.js
- Voronator - upload 3D model, download your voroni tesselated version
- Voronoi experiment @ karljones.com
- Fortune's algorithm for Voronoi diagrams
- Javascript implementation of Steven J. Fortune's algorithm to compute Voronoi diagrams
- Lloyd’s Relaxation - generates a centroidal Voronoi tessellation, which is where the seed point for each Voronoi region is also its centroid
- Voronoi diagram in JavaScript
- Spherical Voronoi Diagram
- Interactive Voronoi Diagram Generator with WebGL
- Voronoi diagram code examples @ rosettacode.org