Template:Are You Sure/January 15: Difference between revisions
No edit summary |
No edit summary |
||
| Line 1: | Line 1: | ||
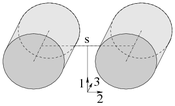
[[File:Kovalevskaya top.png|thumb|175px|link=Kovalevskaya top (nonfiction)|Diagram of a [[Kovalevskaya top (nonfiction)|Kovalevskaya top]], a symmetric top in which two moments of inertia are equal, the third is half as large, and the center of gravity is located in the plane perpendicular to the symmetry axis (parallel to the plane of the two equal points).]] | [[File:Kovalevskaya top.png|thumb|175px|link=Kovalevskaya top (nonfiction)|Diagram of a [[Kovalevskaya top (nonfiction)|Kovalevskaya top]], a symmetric top in which two moments of inertia are equal, the third is half as large, and the center of gravity is located in the plane perpendicular to the symmetry axis (parallel to the plane of the two equal points).]] | ||
• ... that '''[[Johannes Schöner (nonfiction)|Johannes Schöner]]''' was pioneer in the history of globe making, and that he played a significant role in the events | • ... that '''[[Johannes Schöner (nonfiction)|Johannes Schöner]]''' was pioneer in the history of globe making, and that he played a significant role in the events leading up to the publication of Copernicus' ''De revolutionibus'' in 1543?<br> | ||
• ... that a '''[[Kovalevskaya top (nonfiction)|Kovalevskaya top]]''' is a symmetric top in which two moments of inertia are equal, the third is half as large, and the center of gravity is located in the plane perpendicular to the symmetry axis (parallel to the plane of the two equal points)?<br> | • ... that a '''[[Kovalevskaya top (nonfiction)|Kovalevskaya top]]''' is a symmetric top in which two moments of inertia are equal, the third is half as large, and the center of gravity is located in the plane perpendicular to the symmetry axis (parallel to the plane of the two equal points)?<br> | ||
• ... that the '''[[Superimposed Fraunhofer]]''' is a German postage stamp misprint in which the image of Joseph von Fraunhofer appears superimposed on the color spectrum bar, and that the cause of the misprint is thought to originate in as as-yet unidentified [[crime against light]]?<br> | • ... that the '''[[Superimposed Fraunhofer]]''' is a German postage stamp misprint in which the image of Joseph von Fraunhofer appears superimposed on the color spectrum bar, and that the cause of the misprint is thought to originate in as as-yet unidentified [[crime against light]]?<br> | ||
• ... that although '''[[Greedy coloring (nonfiction)|greedy coloring]]''' algorithms do not, in general, use the minimum number of colors possible, they have been used in mathematics as a technique for proving other results about colorings? | • ... that although '''[[Greedy coloring (nonfiction)|greedy coloring]]''' algorithms do not, in general, use the minimum number of colors possible, they have been used in mathematics as a technique for proving other results about colorings? | ||
Revision as of 15:26, 15 January 2020
• ... that Johannes Schöner was pioneer in the history of globe making, and that he played a significant role in the events leading up to the publication of Copernicus' De revolutionibus in 1543?
• ... that a Kovalevskaya top is a symmetric top in which two moments of inertia are equal, the third is half as large, and the center of gravity is located in the plane perpendicular to the symmetry axis (parallel to the plane of the two equal points)?
• ... that the Superimposed Fraunhofer is a German postage stamp misprint in which the image of Joseph von Fraunhofer appears superimposed on the color spectrum bar, and that the cause of the misprint is thought to originate in as as-yet unidentified crime against light?
• ... that although greedy coloring algorithms do not, in general, use the minimum number of colors possible, they have been used in mathematics as a technique for proving other results about colorings?