Gnomon (nonfiction): Difference between revisions
No edit summary |
|||
| Line 2: | Line 2: | ||
The term has come to be used for a variety of purposes in [[mathematics (nonfiction)]] and other fields. | The term has come to be used for a variety of purposes in [[mathematics (nonfiction)]] and other fields. | ||
== History == | |||
Anaximander (610–546 BC) is credited with introducing this Babylonian instrument to the Greeks. | |||
Oenopides used the phrase drawn gnomon-wise to describe a line drawn perpendicular to another. | |||
Later, the term was used for an L-shaped instrument like a steel square used to draw right angles. | |||
This shape may explain its use to describe a shape formed by cutting a smaller square from a larger one (see Hero's definition, below). | |||
Euclid extended the term to the plane figure formed by removing a similar parallelogram from a corner of a larger parallelogram. | |||
Indeed, the gnomon is the increment between two successive figurate numbers, including square and triangular numbers. | |||
== Hero's definition == | |||
[[File:200px-Gnomon.svg.png|thumb|A gnomon as in Euclid book II]] | |||
Hero of Alexandria defined a gnomon as that which, when added to an entity (number or shape), makes a new entity similar to the starting entity. | |||
In this sense Theon of Smyrna used it to describe a number which added to a polygonal number produces the next one of the same type. | |||
The most common use in this sense is an odd integer especially when seen as a figurate number between square numbers. | |||
== China == | |||
The Chinese used the gnomon. | |||
It is mentioned in the 2nd century Nine Chapters on the Mathematical Art as being used much earlier by the Duke of Zhou (11th century BC). | |||
== Computer graphics == | |||
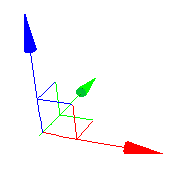
[[File:3DGraphicsGnomon.png|thumb|A gnomon in computer graphics]]A three-dimensional gnomon is commonly used in CAD and computer graphics as an aid to positioning objects in the virtual world. | |||
By convention, colors represent direction: | |||
* The X axis direction is red | |||
* The Y axis is green | |||
* The Z axis is blue | |||
== Nonfiction cross-reference == | == Nonfiction cross-reference == | ||
Revision as of 08:18, 20 May 2016
Gnomon ([ˈnoʊmɒn], from Greek γνώμων, gnōmōn, literally: "one that knows or examines") refers primarily to the part of a sundial (nonfiction) that casts the shadow (nonfiction).
The term has come to be used for a variety of purposes in mathematics (nonfiction) and other fields.
History
Anaximander (610–546 BC) is credited with introducing this Babylonian instrument to the Greeks.
Oenopides used the phrase drawn gnomon-wise to describe a line drawn perpendicular to another.
Later, the term was used for an L-shaped instrument like a steel square used to draw right angles.
This shape may explain its use to describe a shape formed by cutting a smaller square from a larger one (see Hero's definition, below).
Euclid extended the term to the plane figure formed by removing a similar parallelogram from a corner of a larger parallelogram.
Indeed, the gnomon is the increment between two successive figurate numbers, including square and triangular numbers.
Hero's definition
Hero of Alexandria defined a gnomon as that which, when added to an entity (number or shape), makes a new entity similar to the starting entity.
In this sense Theon of Smyrna used it to describe a number which added to a polygonal number produces the next one of the same type.
The most common use in this sense is an odd integer especially when seen as a figurate number between square numbers.
China
The Chinese used the gnomon.
It is mentioned in the 2nd century Nine Chapters on the Mathematical Art as being used much earlier by the Duke of Zhou (11th century BC).
Computer graphics
A three-dimensional gnomon is commonly used in CAD and computer graphics as an aid to positioning objects in the virtual world.
By convention, colors represent direction:
- The X axis direction is red
- The Y axis is green
- The Z axis is blue
Nonfiction cross-reference
Fiction cross-reference
External links
- Gnomon @ Wikipedia