Rod calculus (nonfiction): Difference between revisions
No edit summary |
No edit summary |
||
| Line 2: | Line 2: | ||
Rod calculus played a key role in the development of Chinese mathematics to its height in Song Dynasty and Yuan Dynasty, culminating in the invention of polynomial equations of up to four unknowns in the work of [[Zhu Shijie (nonfiction)|Zhu Shijie]]. | Rod calculus played a key role in the development of Chinese mathematics to its height in Song Dynasty and Yuan Dynasty, culminating in the invention of polynomial equations of up to four unknowns in the work of [[Zhu Shijie (nonfiction)|Zhu Shijie]]. | ||
Counting rods were also used in Japan. | |||
== History == | |||
Chinese arithmeticians used counting rods well over two thousand years ago. In 1954 forty-odd counting rods of the Warring States period (5th century BCE to 221 BCE) were found in Zuǒjiāgōngshān (左家公山) Chu Grave No.15 in Changsha, Hunan. [citation needed] | |||
In 1973 archeologists unearthed a number of wood scripts from a tomb in Hubei dating from the period of the Han dynasty (206 BCE to 220 CE). On one of the wooden scripts was written: "当利二月定算". This is one of the earliest examples of using counting-rod numerals in writing. | |||
In 1976 a bundle of Western Han-era (202 BCE to 9 CE) counting rods made of bones was unearthed from Qianyang County in Shaanxi. The use of counting rods must predate it; Sunzi (c. 544 to c. 496 BCE), a military strategist at the end of Spring and Autumn period of 771 BCE to 5th century BCE, mentions their use to make calculations to win wars before going into the battle; Laozi (died 531 BCE), writing in the Warring States period,[citation needed] said "a good calculator doesn't use counting rods". The Book of Han (finished 111 CE) recorded: "they calculate with bamboo, diameter one fen, length six cun, arranged into a hexagonal bundle of two hundred seventy one pieces". | |||
At first, calculating rods were round in cross-section, but by the time of the Sui dynasty (581 to 618 CE) mathematicians used triangular rods to represent positive numbers and rectangular rods for negative numbers. | |||
After the abacus flourished[when?], counting rods were abandoned except in Japan, where rod numerals developed into a symbolic notation for algebra. | |||
== Using counting rods == | |||
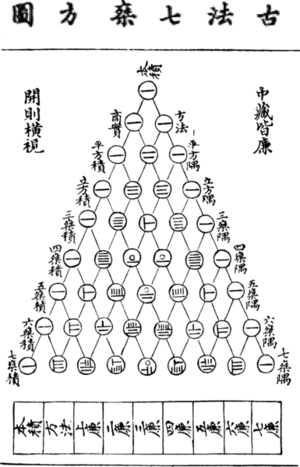
Counting rods represent digits by the number of rods, and the perpendicular rod represents five. To avoid confusion, vertical and horizontal forms are alternately used. Generally, vertical rod numbers are used for the position for the units, hundreds, ten thousands, etc., while horizontal rod numbers are used for the tens, thousands, hundred thousands etc. It is written in Sunzi Suanjing that "one is vertical, ten is horizontal". | |||
Red rods represent positive numbers and black rods represent negative numbers. Ancient Chinese clearly understood negative numbers and zero (leaving a blank space for it), though they had no symbol for the latter. | |||
=== Japan === | |||
In Japan, mathematicians put counting rods on a counting board, a sheet of cloth with grids, and used only vertical forms relying on the grids. An 18th-century Japanese mathematics book has a checker counting board diagram, with the order of magnitude symbols "千百十一分厘毛“(thousand, hundred, ten, unit, tenth, hundredth, thousandth). | |||
The Japanese mathematician [[Seki Takakazu (nonfiction)|Seki Takakazu]] developed the rod numerals into symbolic notation for algebra and drastically improved Japanese mathematics. After his period, the positional numeral system using Chinese numeral characters was developed, and the rod numerals were used only for the plus and minus signs. | |||
== In the News == | == In the News == | ||
| Line 20: | Line 45: | ||
* [[Mathematician (nonfiction)]] | * [[Mathematician (nonfiction)]] | ||
* [[Mathematics (nonfiction)]] | * [[Mathematics (nonfiction)]] | ||
* [[Seki Takakazu (nonfiction)]] | |||
* [[Zhu Shijie (nonfiction)]] | * [[Zhu Shijie (nonfiction)]] | ||
Revision as of 11:33, 23 November 2018
Rod calculus or rod calculation is the mechanical method of algorithmic computation with counting rods in China from the Warring States to Ming dynasty before the counting rods were replaced by the more convenient and faster abacus.
Rod calculus played a key role in the development of Chinese mathematics to its height in Song Dynasty and Yuan Dynasty, culminating in the invention of polynomial equations of up to four unknowns in the work of Zhu Shijie.
Counting rods were also used in Japan.
History
Chinese arithmeticians used counting rods well over two thousand years ago. In 1954 forty-odd counting rods of the Warring States period (5th century BCE to 221 BCE) were found in Zuǒjiāgōngshān (左家公山) Chu Grave No.15 in Changsha, Hunan. [citation needed]
In 1973 archeologists unearthed a number of wood scripts from a tomb in Hubei dating from the period of the Han dynasty (206 BCE to 220 CE). On one of the wooden scripts was written: "当利二月定算". This is one of the earliest examples of using counting-rod numerals in writing.
In 1976 a bundle of Western Han-era (202 BCE to 9 CE) counting rods made of bones was unearthed from Qianyang County in Shaanxi. The use of counting rods must predate it; Sunzi (c. 544 to c. 496 BCE), a military strategist at the end of Spring and Autumn period of 771 BCE to 5th century BCE, mentions their use to make calculations to win wars before going into the battle; Laozi (died 531 BCE), writing in the Warring States period,[citation needed] said "a good calculator doesn't use counting rods". The Book of Han (finished 111 CE) recorded: "they calculate with bamboo, diameter one fen, length six cun, arranged into a hexagonal bundle of two hundred seventy one pieces".
At first, calculating rods were round in cross-section, but by the time of the Sui dynasty (581 to 618 CE) mathematicians used triangular rods to represent positive numbers and rectangular rods for negative numbers.
After the abacus flourished[when?], counting rods were abandoned except in Japan, where rod numerals developed into a symbolic notation for algebra.
Using counting rods
Counting rods represent digits by the number of rods, and the perpendicular rod represents five. To avoid confusion, vertical and horizontal forms are alternately used. Generally, vertical rod numbers are used for the position for the units, hundreds, ten thousands, etc., while horizontal rod numbers are used for the tens, thousands, hundred thousands etc. It is written in Sunzi Suanjing that "one is vertical, ten is horizontal".
Red rods represent positive numbers and black rods represent negative numbers. Ancient Chinese clearly understood negative numbers and zero (leaving a blank space for it), though they had no symbol for the latter.
Japan
In Japan, mathematicians put counting rods on a counting board, a sheet of cloth with grids, and used only vertical forms relying on the grids. An 18th-century Japanese mathematics book has a checker counting board diagram, with the order of magnitude symbols "千百十一分厘毛“(thousand, hundred, ten, unit, tenth, hundredth, thousandth).
The Japanese mathematician Seki Takakazu developed the rod numerals into symbolic notation for algebra and drastically improved Japanese mathematics. After his period, the positional numeral system using Chinese numeral characters was developed, and the rod numerals were used only for the plus and minus signs.
In the News
Fiction cross-reference
Nonfiction cross-reference
- Mathematician (nonfiction)
- Mathematics (nonfiction)
- Seki Takakazu (nonfiction)
- Zhu Shijie (nonfiction)
External links:
- Counting rods @ Wikipedia
- Rod calculus @ Wikipedia