Rod calculus (nonfiction): Difference between revisions
Jump to navigation
Jump to search
No edit summary |
No edit summary |
||
| Line 1: | Line 1: | ||
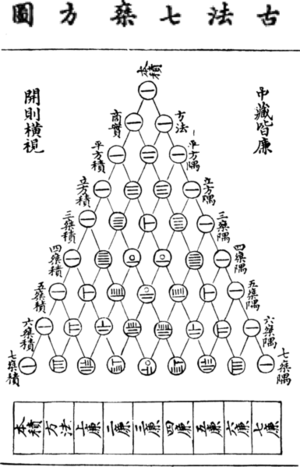
[[File:Japanese_counting_board.jpg|thumb|Japanese counting board with grids.]]'''Rod calculus''' or '''rod calculation''' is the mechanical method of algorithmic computation with counting rods in China from the Warring States to Ming dynasty before the counting rods were replaced by the more convenient and faster abacus. | [[File:Yanghui triangle.gif|thumb|Yang Hui triangle, as depicted by Zhu Shijie in 1303, using rod numerals.]][[File:Japanese_counting_board.jpg|thumb|Japanese counting board with grids.]]'''Rod calculus''' or '''rod calculation''' is the mechanical method of algorithmic computation with counting rods in China from the Warring States to Ming dynasty before the counting rods were replaced by the more convenient and faster abacus. | ||
Rod calculus played a key role in the development of Chinese mathematics to its height in Song Dynasty and Yuan Dynasty, culminating in the invention of polynomial equations of up to four unknowns in the work of [[Zhu Shijie (nonfiction)|Zhu Shijie]]. | Rod calculus played a key role in the development of Chinese mathematics to its height in Song Dynasty and Yuan Dynasty, culminating in the invention of polynomial equations of up to four unknowns in the work of [[Zhu Shijie (nonfiction)|Zhu Shijie]]. | ||
| Line 24: | Line 24: | ||
External links: | External links: | ||
* [https://en.wikipedia.org/wiki/Counting_rods Counting rods] @ Wikipedia | |||
* [https://en.wikipedia.org/wiki/Rod_calculus Rod calculus] @ Wikipedia | * [https://en.wikipedia.org/wiki/Rod_calculus Rod calculus] @ Wikipedia | ||
[[Category:Nonfiction (nonfiction)]] | [[Category:Nonfiction (nonfiction)]] | ||
[[Category:Mathematics (nonfiction)]] | [[Category:Mathematics (nonfiction)]] | ||
Revision as of 11:25, 23 November 2018
Rod calculus or rod calculation is the mechanical method of algorithmic computation with counting rods in China from the Warring States to Ming dynasty before the counting rods were replaced by the more convenient and faster abacus.
Rod calculus played a key role in the development of Chinese mathematics to its height in Song Dynasty and Yuan Dynasty, culminating in the invention of polynomial equations of up to four unknowns in the work of Zhu Shijie.
In the News
Fiction cross-reference
Nonfiction cross-reference
External links:
- Counting rods @ Wikipedia
- Rod calculus @ Wikipedia