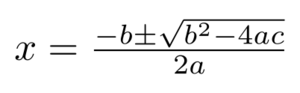Quadratic equation

The quadratic formula for the roots of the general quadratic equation.

In algebra, a quadratic equation (from the Latin quadratus for "square") is any equation having the form ax^2+bx+c=0 where x represents an unknown, and a, b, and c represent known numbers such that a is not equal to 0.

If a = 0, then the equation is linear, not quadratic.

The numbers a, b, and c are the coefficients of the equation, and may be distinguished by calling them, respectively, the quadratic coefficient, the linear coefficient and the constant or free term.

Because the quadratic equation involves only one unknown, it is called "univariate". The quadratic equation only contains powers of x that are non-negative integers, and therefore it is a polynomial equation, and in particular it is a second degree polynomial equation since the greatest power is two.

Quadratic equations can be solved by a process known in American English as factoring and in other varieties of English as factorizing, by completing the square, by using the quadratic formula, or by graphing.

Solutions to problems equivalent to the quadratic equation were known as early as 2000 BC.

Fiction cross-reference

• Gnomon algorithm
• Mathematics

Nonfiction cross-reference

• Algebra (nonfiction)
• Linear equation (nonfiction)
• Mathematics (nonfiction)
• Quadratic formula (nonfiction)

External links:

• Quadratic equation @ Wikipedia