Crank–Nicolson method (nonfiction): Difference between revisions
No edit summary |
|||
| (8 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
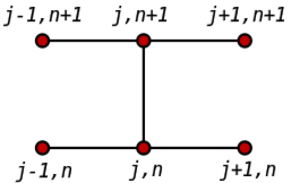
[[File:Crank-Nicolson-stencil.svg|thumb|The Crank–Nicolson stencil for a 1D problem.]]In numerical analysis, the '''Crank–Nicolson method''' is a finite difference method used for numerically solving the heat equation and similar [[Partial differential equation (nonfiction)|partial differential equations]]. | |||
== Description == | == Description == | ||
| Line 5: | Line 5: | ||
It is a second-order method in time, it is implicit in time and can be written as an implicit Runge–Kutta method, and it is numerically stable. | It is a second-order method in time, it is implicit in time and can be written as an implicit Runge–Kutta method, and it is numerically stable. | ||
The method was developed by John Crank and Phyllis Nicolson in the mid 20th century. | The method was developed by [[John Crank (nonfiction)|John Crank]] and [[Phyllis Nicolson (nonfiction)|Phyllis Nicolson]] in the mid 20th century. | ||
For diffusion equations (and many other equations), it can be shown the Crank–Nicolson method is unconditionally stable. | For diffusion equations (and many other equations), it can be shown the Crank–Nicolson method is unconditionally stable. | ||
| Line 12: | Line 12: | ||
For this reason, whenever large time steps or high spatial resolution is necessary, the less accurate backward Euler method is often used, which is both stable and immune to oscillations. | For this reason, whenever large time steps or high spatial resolution is necessary, the less accurate backward Euler method is often used, which is both stable and immune to oscillations. | ||
== In the News == | |||
<gallery> | |||
</gallery> | |||
== Fiction cross reference == | |||
* [[Crimes against mathematical constants]] | |||
* [[Gnomon algorithm]] | |||
* [[Mathematics]] | |||
== Nonfiction cross reference == | == Nonfiction cross reference == | ||
* [[John Crank (nonfiction)]] | |||
* [[Phyllis Nicolson (nonfiction)]] | |||
* [[Numerical analysis (nonfiction)]] | * [[Numerical analysis (nonfiction)]] | ||
* [[Partial differential equation (nonfiction)]] | |||
== | == External links == | ||
* [https://en.wikipedia.org/wiki/Crank%E2%80%93Nicolson_method Crank–Nicolson method] | |||
[[Category:Nonfiction (nonfiction)]] | |||
[[Category:Mathematics (nonfiction)]] | |||
[[Category:Numerical analysis (nonfiction)]] | |||
Latest revision as of 06:15, 4 September 2024
In numerical analysis, the Crank–Nicolson method is a finite difference method used for numerically solving the heat equation and similar partial differential equations.
Description
It is a second-order method in time, it is implicit in time and can be written as an implicit Runge–Kutta method, and it is numerically stable.
The method was developed by John Crank and Phyllis Nicolson in the mid 20th century.
For diffusion equations (and many other equations), it can be shown the Crank–Nicolson method is unconditionally stable.
However, the approximate solutions can still contain (decaying) spurious oscillations if the ratio of time step Δt times the thermal diffusivity to the square of space step, Δx2, is large (typically larger than 1/2 per Von Neumann stability analysis).
For this reason, whenever large time steps or high spatial resolution is necessary, the less accurate backward Euler method is often used, which is both stable and immune to oscillations.
In the News
Fiction cross reference
Nonfiction cross reference
- John Crank (nonfiction)
- Phyllis Nicolson (nonfiction)
- Numerical analysis (nonfiction)
- Partial differential equation (nonfiction)