Halting problem (nonfiction): Difference between revisions
No edit summary |
|||
| Line 10: | Line 10: | ||
<gallery mode="traditional"> | <gallery mode="traditional"> | ||
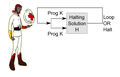
File:Ascleplius Myrmidon Halting Problem.jpg|link=On Halting | File:Ascleplius Myrmidon Halting Problem.jpg|link=On Halting Problems|[[On Halting Problems|Asclepius Myrmidon discovers unregistered halting problem]], predicts new class of [[crimes against mathematical constants]]. | ||
File:Forbidden_Ratio_symbol.jpg|link=Forbidden Ratio and Gnotilus (crime team)|Supervillains [[Forbidden Ratio and Gnotilus (crime team)|Forbidden Ratio and Gnotilus]] threaten to [[Weaponization (nonfiction)|weaponize]] new class of Halting problems. | File:Forbidden_Ratio_symbol.jpg|link=Forbidden Ratio and Gnotilus (crime team)|Supervillains [[Forbidden Ratio and Gnotilus (crime team)|Forbidden Ratio and Gnotilus]] threaten to [[Weaponization (nonfiction)|weaponize]] new class of Halting problems. | ||
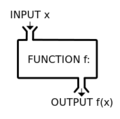
File:Mathematical function.svg|link=Mathematical function (nonfiction)|Law-abiding [[Mathematical function (nonfiction)|mathematical functions]] have nothing to fear from [[Crimes against mathematical constants]], say crime authorities. | File:Mathematical function.svg|link=Mathematical function (nonfiction)|Law-abiding [[Mathematical function (nonfiction)|mathematical functions]] have nothing to fear from [[Crimes against mathematical constants]], say crime authorities. | ||
Revision as of 13:29, 24 January 2017
In computability theory, the halting problem is the problem of determining, from a description of an arbitrary computer program and an input, whether the program will finish running or continue to run forever. See Computation (nonfiction).
Alan Turing proved in 1936 that a general algorithm to solve the halting problem for all possible program-input pairs cannot exist.
A key part of the proof was a mathematical definition of a computer and program, which became known as a Turing machine; the halting problem is undecidable over Turing machines.
It is one of the first examples of a decision problem.
In the News
Asclepius Myrmidon discovers unregistered halting problem, predicts new class of crimes against mathematical constants.
Supervillains Forbidden Ratio and Gnotilus threaten to weaponize new class of Halting problems.
Law-abiding mathematical functions have nothing to fear from Crimes against mathematical constants, say crime authorities.
Fiction cross-reference
Nonfiction cross-reference
- Computation (nonfiction)
- Computer science (nonfiction)
- Weapon (nonfiction)
- Weaponization (nonfiction)
External links:
- Halting problem @ Wikipedia