Lorenz system (nonfiction): Difference between revisions
Jump to navigation
Jump to search
No edit summary |
|||
| (10 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
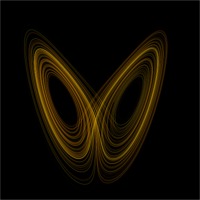
The '''Lorenz system''' is a system of ordinary differential equation (the Lorenz equations) first studied by Edward Lorenz. | [[File:Lorenz_attractor_trajectory-through-phase-space.gif|frame|A sample solution in the Lorenz attractor when ρ = 28, σ = 10, and β = 8/3]]The '''Lorenz system''' is a system of ordinary differential equation (the Lorenz equations) first studied by Edward Lorenz. | ||
It is notable for having chaotic solutions for certain parameter values and initial conditions. | It is notable for having chaotic solutions for certain parameter values and initial conditions. | ||
In particular, the Lorenz attractor is a set of chaotic solutions of the Lorenz system which, when plotted, resemble a butterfly or figure eight. | In particular, the Lorenz attractor is a set of chaotic solutions of the Lorenz system which, when plotted, resemble a butterfly or figure eight. | ||
== In the News == | |||
<gallery mode="traditional" widths="200px" heights="200px"> | |||
File:Hamangia-figures-Lorenz-attractor.jpg|link=Hamangia scrying engine|[[Hamangia scrying engine|Hamangia figurines]] computing the Lorenz system. | |||
File:Lorenz attractor.png|link=Chaos theory (nonfiction)|New autobiography of [[Chaos theory (nonfiction)|Chaos theory]] remembers [[Edward Lorenz (nonfiction)|Edward Lorenz]] as quiet genius. | |||
</gallery> | |||
== Fiction cross-reference == | |||
== Nonfiction cross-reference == | == Nonfiction cross-reference == | ||
| Line 13: | Line 20: | ||
* [[Mathematics (nonfiction)]] | * [[Mathematics (nonfiction)]] | ||
External links: | |||
* [https://en.wikipedia.org/wiki/Lorenz_system Lorenz system] @ Wikipedia | * [https://en.wikipedia.org/wiki/Lorenz_system Lorenz system] @ Wikipedia | ||
Latest revision as of 08:29, 18 December 2016
A sample solution in the Lorenz attractor when ρ = 28, σ = 10, and β = 8/3
The Lorenz system is a system of ordinary differential equation (the Lorenz equations) first studied by Edward Lorenz.
It is notable for having chaotic solutions for certain parameter values and initial conditions.
In particular, the Lorenz attractor is a set of chaotic solutions of the Lorenz system which, when plotted, resemble a butterfly or figure eight.
In the News
Hamangia figurines computing the Lorenz system.
New autobiography of Chaos theory remembers Edward Lorenz as quiet genius.
Fiction cross-reference
Nonfiction cross-reference
External links:
- Lorenz system @ Wikipedia