Chaos theory (nonfiction): Difference between revisions
(Created page with "In mathematics, '''chaos theory''' refers to the behavior of dynamical systems that are highly sensitive to initial conditions -- a response popul...") |
No edit summary |
||
| Line 1: | Line 1: | ||
In [[Mathematics (nonfiction)|mathematics]], '''chaos theory''' refers to the behavior of dynamical systems that are highly sensitive to initial conditions -- a response popularly referred to as the butterfly effect. | [[File:Lorenz_attractor.png|thumb|Visualization of a [[Lorenz attractor (nonfiction)|Lorenz attractor]], one of the classic images of chaos theory.]]In [[Mathematics (nonfiction)|mathematics]], '''chaos theory''' refers to the behavior of dynamical systems that are highly sensitive to initial conditions -- a response popularly referred to as the butterfly effect. | ||
Small differences in initial conditions (such as those due to rounding errors in [[Computation (nonfiction)|numerical computation]]) yield widely diverging outcomes for such dynamical systems, rendering long-term prediction impossible in general. | Small differences in initial conditions (such as those due to rounding errors in [[Computation (nonfiction)|numerical computation]]) yield widely diverging outcomes for such dynamical systems, rendering long-term prediction impossible in general. | ||
| Line 14: | Line 14: | ||
<gallery mode="traditional" widths="200px" heights="200px"> | <gallery mode="traditional" widths="200px" heights="200px"> | ||
File:Edward Lorenz.jpg|link=Edward Lorenz (nonfiction)|[[Edward Lorenz (nonfiction)|Edward Lorenz]] hailed as pioneer of chaos theory. | |||
</gallery> | </gallery> | ||
== Fiction cross-reference == | == Fiction cross-reference == | ||
* [[]] | |||
== Nonfiction cross-reference == | == Nonfiction cross-reference == | ||
* [[Edward Lorenz (nonfiction)]] | |||
* [[Mathematics (nonfiction)]] | * [[Mathematics (nonfiction)]] | ||
Revision as of 08:20, 18 December 2016
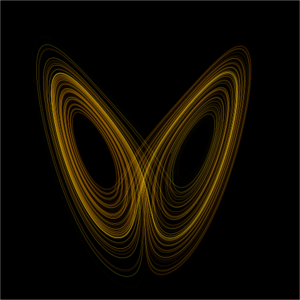
In mathematics, chaos theory refers to the behavior of dynamical systems that are highly sensitive to initial conditions -- a response popularly referred to as the butterfly effect.
Small differences in initial conditions (such as those due to rounding errors in numerical computation) yield widely diverging outcomes for such dynamical systems, rendering long-term prediction impossible in general.
This happens even though these systems are deterministic, meaning that their future behavior is fully determined by their initial conditions, with no random elements involved.
In other words: the deterministic nature of these systems does not make them predictable.
The theory was summarized by Edward Norton Lorenz as:
Chaos: When the present determines the future, but the approximate present does not approximately determine the future.
In the News
Edward Lorenz hailed as pioneer of chaos theory.
Fiction cross-reference
- [[]]
Nonfiction cross-reference
External links:
- Chaos theory @ Wikipedia
