Cantor's diagonal argument (nonfiction): Difference between revisions
(Created page with "File:Cantor's_diagonal_argument.svg|thumb|An illustration of Cantor's diagonal argument (in base 2) for the existence of uncountable sets. The sequence at the bottom cannot...") |
No edit summary |
||
| Line 1: | Line 1: | ||
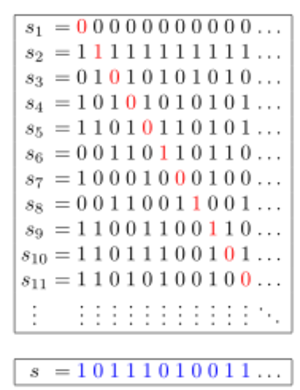
[[File:Cantor's_diagonal_argument.svg|thumb|An illustration of Cantor's diagonal argument (in base 2) for the existence of uncountable sets. The sequence at the bottom cannot occur anywhere in the enumeration of sequences above.]]In [[Set theory (nonfiction)|set theory | [[File:Cantor's_diagonal_argument.svg|thumb|An illustration of Cantor's diagonal argument (in base 2) for the existence of uncountable sets. The sequence at the bottom cannot occur anywhere in the enumeration of sequences above.]]In [[Set theory (nonfiction)|set theory]], '''Cantor's diagonal argument''', also called the '''diagonalization argument''', the '''diagonal slash argument''' or the '''diagonal method''', was published in 1891 by [[Georg Cantor (nonfiction)|Georg Cantor]] as a mathematical proof that there are infinite sets which cannot be put into one-to-one correspondence with the infinite set of [[Natural number (nonfiction)|natural numbers]]. | ||
Such sets are now known as uncountable sets, and the size of infinite sets is now treated by the theory of cardinal numbers which Cantor began. | Such sets are now known as uncountable sets, and the size of infinite sets is now treated by the theory of cardinal numbers which Cantor began. | ||
Latest revision as of 17:32, 14 November 2017
In set theory, Cantor's diagonal argument, also called the diagonalization argument, the diagonal slash argument or the diagonal method, was published in 1891 by Georg Cantor as a mathematical proof that there are infinite sets which cannot be put into one-to-one correspondence with the infinite set of natural numbers.
Such sets are now known as uncountable sets, and the size of infinite sets is now treated by the theory of cardinal numbers which Cantor began.
The diagonal argument was not Cantor's first proof of the uncountability of the real numbers, which appeared in 1874. However, the diagonal argument demonstrates a powerful and general technique that has since been used in a wide range of proofs, including the first of Gödel's incompleteness theorems and Alan Turing's answer to the Entscheidungsproblem.
Diagonalization arguments are often also the source of contradictions like Russell's paradox and Richard's paradox.
Historically, the diagonal argument first appeared in the work of Paul du Bois-Reymond in 1875.
In the News
Fiction cross-reference
Nonfiction cross-reference
- Georg Cantor (nonfiction)
- Mathematics (nonfiction)
- Natural number (nonfiction)
- Paul du Bois-Reymond (nonfiction)
- Set theory (nonfiction)
External links:
- Cantor's diagonal argument @ Wikipedia