E (nonfiction): Difference between revisions
No edit summary |
No edit summary |
||
| (14 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
[[File:E_hyperbola.svg|thumb|The graph is y=1/x, and ''e'' is the unique [[Irrational number (nonfiction)|irrational number]] that makes the shaded area equal to 1.]]The number '''''e''''' is a mathematical constant that is the base of the natural logarithm: the unique number whose natural logarithm is equal to one. | |||
The number '''''e''''' is a mathematical constant that is the base of the natural logarithm: the unique number whose natural logarithm is equal to one. | |||
It is approximately equal to 2.71828, and is the limit of (1 + 1/n)n as n approaches infinity, an expression that arises in the study of compound interest. | It is approximately equal to 2.71828, and is the limit of (1 + 1/n)n as n approaches infinity, an expression that arises in the study of compound interest. | ||
| Line 12: | Line 11: | ||
The natural logarithm, or logarithm to base e, is the inverse function to the natural exponential function. | The natural logarithm, or logarithm to base e, is the inverse function to the natural exponential function. | ||
Sometimes called '''Euler's number''' after the Swiss mathematician [[Leonhard Euler (nonfiction)|Leonhard Euler]], e is not to be confused with γ, the Euler–Mascheroni constant, sometimes called simply Euler's constant. The number e is also known as Napier's constant, | Sometimes called '''Euler's number''' after the Swiss mathematician [[Leonhard Euler (nonfiction)|Leonhard Euler]], ''e'' is not to be confused with γ, the Euler–Mascheroni constant, sometimes called simply Euler's constant. | ||
The number e is also known as Napier's constant, Euler's choice of the symbol ''e'' is said to have been retained in his honor. | |||
The constant was discovered by the Swiss mathematician [[Jacob Bernoulli (nonfiction)|Jacob Bernoulli]] while studying compound interest. | |||
The number e is of eminent importance in mathematics, alongside 0, 1, [[Pi (nonfiction)|π]], and i. All five of these numbers play important and recurring roles across mathematics, and are the five constants appearing in one formulation of Euler's identity. Like the constant [[Pi (nonfiction)|π]], e is an [[Irrational number (nonfiction)|irrational number]]: it is not a ratio of integers. | The number e is of eminent importance in mathematics, alongside 0, 1, [[Pi (nonfiction)|π]], and i. All five of these numbers play important and recurring roles across mathematics, and are the five constants appearing in one formulation of Euler's identity. Like the constant [[Pi (nonfiction)|π]], e is an [[Irrational number (nonfiction)|irrational number]]: it is not a ratio of integers. | ||
| Line 24: | Line 27: | ||
== Fiction cross-reference == | == Fiction cross-reference == | ||
* [[Crimes against mathematical constants]] | |||
== Nonfiction cross-reference == | == Nonfiction cross-reference == | ||
* [[Irrational number (nonfiction)]] | |||
* [[Jacob Bernoulli (nonfiction)]] | |||
* [[Leonhard Euler (nonfiction)]] | * [[Leonhard Euler (nonfiction)]] | ||
* [[Mathematics (nonfiction)]] | * [[Mathematics (nonfiction)]] | ||
| Line 33: | Line 40: | ||
External links: | External links: | ||
* [https://en.wikipedia.org/wiki/E_(mathematical_constant) e (mathematical constant] @ Wikipedia | * [https://en.wikipedia.org/wiki/E_(mathematical_constant) e (mathematical constant)] @ Wikipedia | ||
[[Category:Nonfiction (nonfiction)]] | [[Category:Nonfiction (nonfiction)]] | ||
[[Category:Mathematics (nonfiction)]] | [[Category:Mathematics (nonfiction)]] | ||
{{ | {{E}} | ||
Latest revision as of 11:18, 14 November 2017
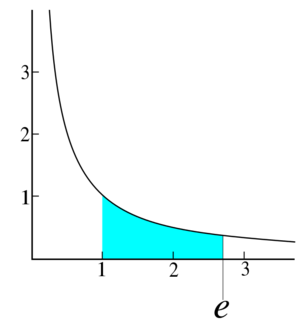
The number e is a mathematical constant that is the base of the natural logarithm: the unique number whose natural logarithm is equal to one.
It is approximately equal to 2.71828, and is the limit of (1 + 1/n)n as n approaches infinity, an expression that arises in the study of compound interest.
It can also be calculated as the sum of an infinite series.
The constant can be characterized in many different ways. For example, e can be defined as the unique positive number a such that the graph of the function y = ax has unit slope at x = 0.
The function f(x) = ex is called the (natural) exponential function.
The natural logarithm, or logarithm to base e, is the inverse function to the natural exponential function.
Sometimes called Euler's number after the Swiss mathematician Leonhard Euler, e is not to be confused with γ, the Euler–Mascheroni constant, sometimes called simply Euler's constant.
The number e is also known as Napier's constant, Euler's choice of the symbol e is said to have been retained in his honor.
The constant was discovered by the Swiss mathematician Jacob Bernoulli while studying compound interest.
The number e is of eminent importance in mathematics, alongside 0, 1, π, and i. All five of these numbers play important and recurring roles across mathematics, and are the five constants appearing in one formulation of Euler's identity. Like the constant π, e is an irrational number: it is not a ratio of integers.
Also like π, e is transcendental: it is not a root of any non-zero polynomial with rational coefficients.
In the News
Fiction cross-reference
Nonfiction cross-reference
- Irrational number (nonfiction)
- Jacob Bernoulli (nonfiction)
- Leonhard Euler (nonfiction)
- Mathematics (nonfiction)
- Pi (nonfiction)
External links:
- e (mathematical constant) @ Wikipedia