Greedy algorithm (nonfiction): Difference between revisions
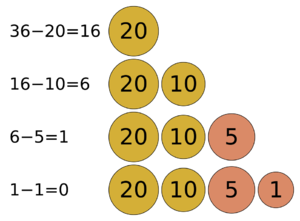
(Created page with "File:Greedy_algorithm_36_cents.svg|thumb|Greedy algorithms determine minimum number of coins to give while making change. These are the steps a human would take to emulate a...") |
No edit summary |
||
| Line 24: | Line 24: | ||
External links: | External links: | ||
* [https://en.wikipedia.org/wiki/ | * [https://en.wikipedia.org/wiki/Greedy_algorithm Greedy algorithm] @ Wikipedia | ||
[[Category:Nonfiction (nonfiction)]] | [[Category:Nonfiction (nonfiction)]] | ||
[[Category:Algorithms (nonfiction)]] | [[Category:Algorithms (nonfiction)]] | ||
[[Category:Mathematicians (nonfiction)]] | [[Category:Mathematicians (nonfiction)]] | ||
Revision as of 10:55, 3 September 2018
A greedy algorithm is an algorithmic paradigm that follows the problem solving heuristic of making the locally optimal choice at each stage with the intent of finding a global optimum. In many problems, a greedy strategy does not usually produce an optimal solution, but nonetheless a greedy heuristic may yield locally optimal solutions that approximate a globally optimal solution in a reasonable amount of time.
For example, a greedy strategy for the traveling salesman problem (which is of a high computational complexity) is the following heuristic: "At each step of the journey, visit the nearest unvisited city." This heuristic doesn't intend to find a best solution, but it terminates in a reasonable number of steps; finding an optimal solution to such a complex problem typically requires unreasonably many steps. In mathematical optimization, greedy algorithms optimally solve combinatorial problems having the properties of matroids, and give constant-factor approximations to optimization problems with submodular structure.
In the News
Fiction cross-reference
Nonfiction cross-reference
- Algorithm (nonfiction)
- Algorithmic paradigm (nonfiction)
- Greedy coloring (nonfiction)
- Mathematics (nonfiction)
External links:
- Greedy algorithm @ Wikipedia