E (nonfiction)

The graph is y=1/x, and e is the unique irrational number that makes the shaded area equal to 1.

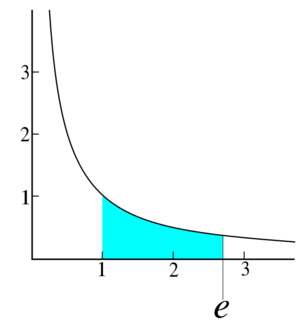
The number e is a mathematical constant that is the base of the natural logarithm: the unique number whose natural logarithm is equal to one.

It is approximately equal to 2.71828, and is the limit of (1 + 1/n)n as n approaches infinity, an expression that arises in the study of compound interest.

It can also be calculated as the sum of an infinite series.

The constant can be characterized in many different ways. For example, e can be defined as the unique positive number a such that the graph of the function y = ax has unit slope at x = 0.

The function f(x) = ex is called the (natural) exponential function.

The natural logarithm, or logarithm to base e, is the inverse function to the natural exponential function.

Sometimes called Euler's number after the Swiss mathematician Leonhard Euler, e is not to be confused with γ, the Euler–Mascheroni constant, sometimes called simply Euler's constant. The number e is also known as Napier's constant, but Euler's choice of the symbol e is said to have been retained in his honor.[4] The constant was discovered by the Swiss mathematician Jacob Bernoulli while studying compound interest.

The number e is of eminent importance in mathematics, alongside 0, 1, π, and i. All five of these numbers play important and recurring roles across mathematics, and are the five constants appearing in one formulation of Euler's identity. Like the constant π, e is an irrational number: it is not a ratio of integers.

Also like π, e is transcendental: it is not a root of any non-zero polynomial with rational coefficients.

Fiction cross-reference

• Crimes against mathematical constants

Nonfiction cross-reference

• Leonhard Euler (nonfiction)
• Mathematics (nonfiction)
• Pi (nonfiction)

External links:

• e (mathematical constant @ Wikipedia